なぜRPN電卓が良いのか?
RPN(Reverse Polish Notation、逆ポーランド記法)電卓の製造をヒューレット・パッカード社がやめ、入手が難しくなったことで、ますますRPN電卓の認知度が減少している。いまでもRPN電卓を支持するユーザーは多いが、彼らからは、RPNでない電卓など使えたものではない、RPNの良さは使ってみればわかる、というような極端な意見も見られ、これでは新たなファンの広がりようがない。一方、RPN電卓の良さを知らず、触れる機会もない大多数のユーザーにとっては、数式通り入力のなにがいけないのか、という疑問があるのは当然で、それに対する十分な説明が不足しているようにも思われる。そこでここでは、いまさらながらに、RPN電卓の良さについて詳細に説明してみたい。
RPN電卓の良さは、以下のような点にあると考えられる。
- 計算手順の統一性が高く、迷いなく操作できる
- 計算結果を簡単に再利用できる
- 演算子の優先順位を気にする必要がない
- 計算中に中間結果を確認しやすい
- アンドゥ機能との親和性が高い
操作手順の統一性が高い
まずは、数式通り関数電卓の操作法について、いくつかの例を見ていただきたい。
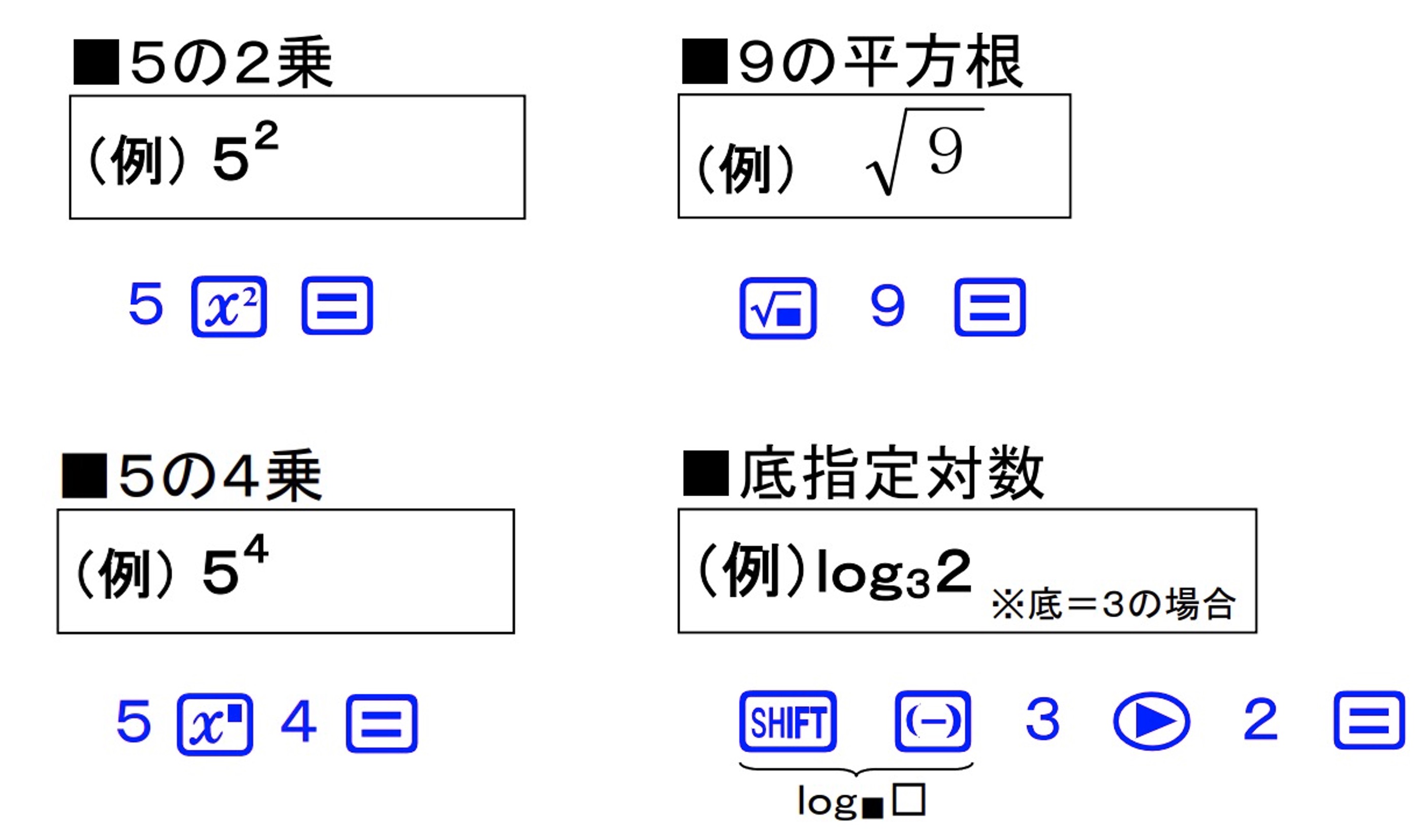
カシオ モノクロ関数電卓(JP500)説明資料から引用
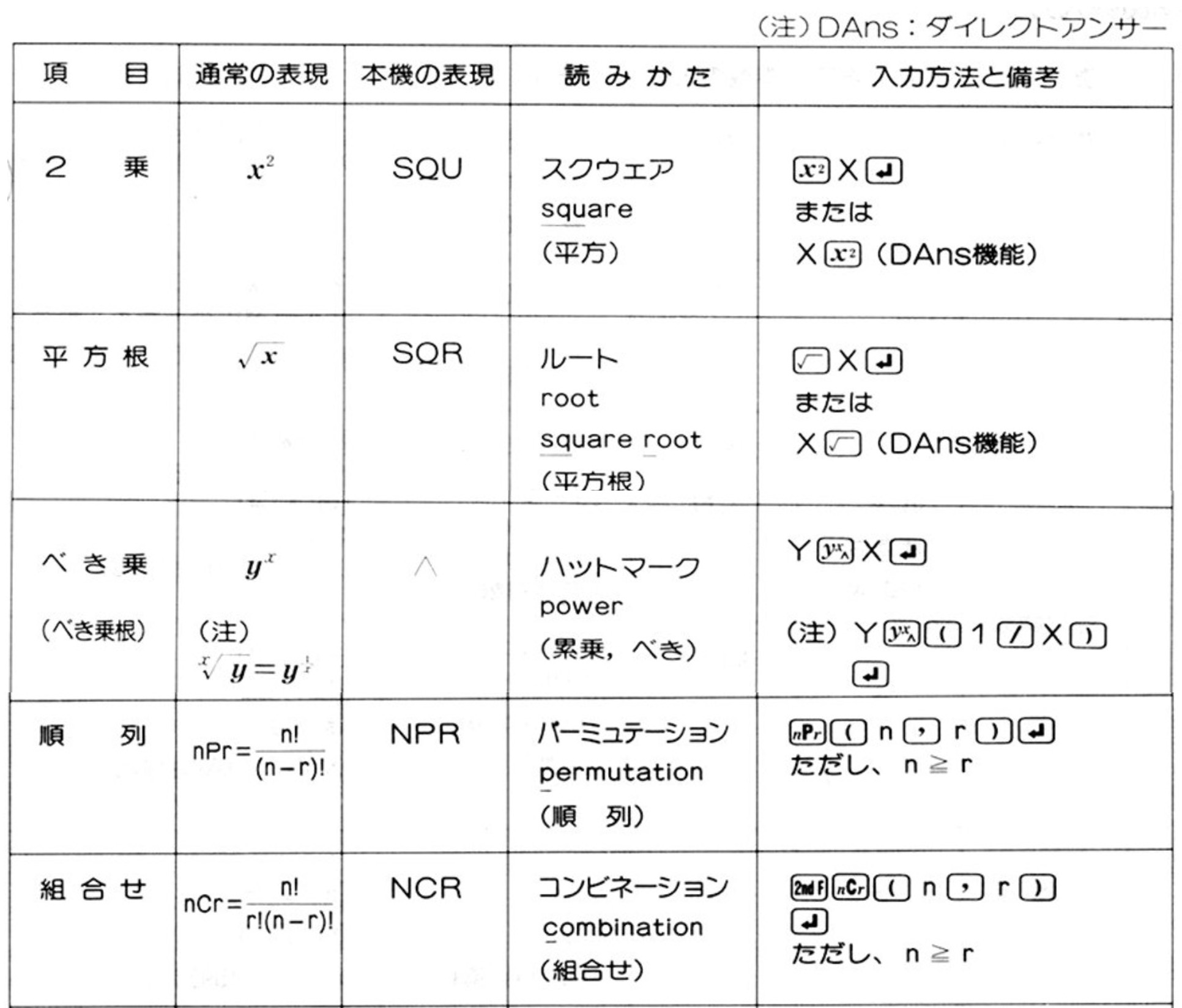
シャープ PC-G801 説明書から引用
いずれの電卓も、演算子の位置を前置・中置・後置のいずれにするかが統一されておらず、また複数の手段が用意されていたりもする。関数電卓に多い単項演算については、前者(カシオ)の例では、互いに逆関数の関係にある2乗が後置、平方根が前置となっている。後者(シャープ)のポケコンでは前置と後置の両方が使用できるが、後置の入力方式をわざわざDAns機能と命名して売り物にしているところに、すでにRPN(=後置)の利点が見え隠れする。
二項演算子ではどうだろうか。二項演算を自然に入力、記述できそうな数式通り入力(中置記法)であるが、四則演算以外ではかえってやっかいである。カシオの例ではべき乗$y^x$の入力方法が中置記法になっているが、その逆関数の底指定対数$\log_y x$は前置記法である。シャープの電卓ではべき乗が中置、順列・組み合わせが前置で、底指定対数は用意されていない。つまり、これらの電卓では統一された操作方法を提供できていない。ボタンの表記などで工夫されているものもあるが、計算中に各関数の入力方法にいちいち注意を払わないといけないのはストレスの元になる。
これに対しRPN電卓では、関数や演算子は後置で統一されており、その対象となる数値の順序も明確に示しやすい。

左:自作の木製RPN電卓のファンクション表示例
右:Hewlett Packard HP-42S (by Andy / Andrew Fogg)
上はRPN電卓の関数の表示例である。この方式では、$\log$や$10^x$のような単項演算はもちろん、$\log_y x$や$y^x$のような二項演算子も自然に操作できる。特にこれらの電卓ではスタックが常時、2段以上表示され、それに先頭から $x$, $y$ の記号を振ってある。これを関数表記に含めているため、どの数値がどこに作用するのかが一目瞭然である(単項演算子では演算対象が$x$であることが明確なので、割愛している場合もある)。当然、左の例では$\log_y x$を押すと$\log_2 3$が、また$y^x$を押すと$2^3$が計算される。
ホビーRPN電卓の自作のファームウェア紹介
余談ではあるが、ほとんどの演算が二項演算までであることから(RPNでは3項以上の演算操作も明快であるが)、RPN電卓のスタック表示は最低2段分欲しい。1段表示のHP-10CシリーズやHP-32Sにも人気があるが、それよりもHP-42Sが熱烈に支持されているのは、2段表示で、画面上に x, yが表示されていることがその一因だろう。小型のホビーRPN電卓も、自作のファームウェアでは全て2段表示に改良している。
演算結果の再利用が簡単
RPN電卓の演算子が常に後置であることは、演算結果の再利用の簡単さに直結している。というのは、前置記法や中置記法では演算子($\log$や$\sin$など)を入れてから数値を入力しなければならないため、数値の再利用を行うためにはなんらか特別なメモリー機能が必要になるためである。実際、多くの「数式通り」関数電卓にはANSキー(アンサーメモリー)など、直前の演算結果を再利用できる機能がついている。通常の電卓でもM+, M-, MRなどのメモリー機能が搭載されているものが多い。しかし、これらのメモリーは多くの場合、1つしかないため、2つ以上の値を再利用して計算するには、後述するプリアンサーメモリーか、A, Bなどの変数メモリー機能が必要になってしまう。
この問題は単項演算ではあまり気にならないことが多い。実際、多くの関数電卓では、単項演算($\sin(x)$や$\sqrt{x}$など)は後置記法で、つまり画面に出ている数値に対して関数を適用する形で実行できるようになっている。しかし、二項演算ではそうもいかない。前述の$\log_y x$や$y^x$のような場合に限らず、最後の計算が四則演算であるときも同様である。なんらかの計算が分母と分子にあり、それらを最後に除算したいときに面倒が生じるわけである。つまり例えば、
| \[ \frac{92 - 44}{78 - 56} \] |
これは前述のM+, M-, MRを使えば解決するではないか、という意見もあるだろう。分母の計算をまず行い、これをM+に記憶しておく。次に分子の計算を行ってから、/ MR =と操作すれば、確かに目的は達成できる。しかし、その間にうっかりCやMCでなくACを押してしまい、やり直しになってしまったことはないだろうか?また、計算順序が逆になってしまったときの対処もちょっとしたストレスになる。最後の計算が減算や除算の場合は、計算後に符号反転や逆数の計算で解決できるが、$\log_y x$や$y^x$のときはそうも行かない。
それに対しRPNでは、単に必要な数値を計算していき、それらをスタックに積み上げるだけで演算結果を自由に再利用できる。そして得られた結果が最後の演算に対して逆に並んでしまっても、SWAPを実行すれば簡単に入れ替えられるので、特に順序など気にせず計算していっても、ストレスなく再利用が容易である。また後述するように、分母・分子の値を確認してから次の演算を行うこともできる(数式通り入力で、括弧を用いて一気に計算するときはそうもいかない)。
通常の電卓では結局、脇にメモ帳を置いて計算することも多い。最近は電子メモパッドが一体化された電卓も多く発売されている。だが、RPNではこのようなメモが必要になる頻度が低く、快適に計算ができる。最近の関数電卓には2つ前の計算結果を記憶するプリアンサーメモリーなる機能まで登場しているが、複雑な計算を行うと失われてしまうわけだし、第一、そんな薄氷を踏むように間違いなく電卓を操作しなければならないのはいやである。そもそも、「2つ前を記憶する」などという考え方そのものが、RPNにおける「スタック」の概念へ(中途半端に)近づいているのだ。
演算子の優先順位を気にしなくてよい
RPN電卓では「括弧を入力する必要がない」ことがそのメリットのひとつに挙げられることがある。しかしこれは(間違いではないが)やや舌足らずな説明である。ここではRPNの利点を語るときによく例として用いられる、台形の面積の計算を例に説明する。
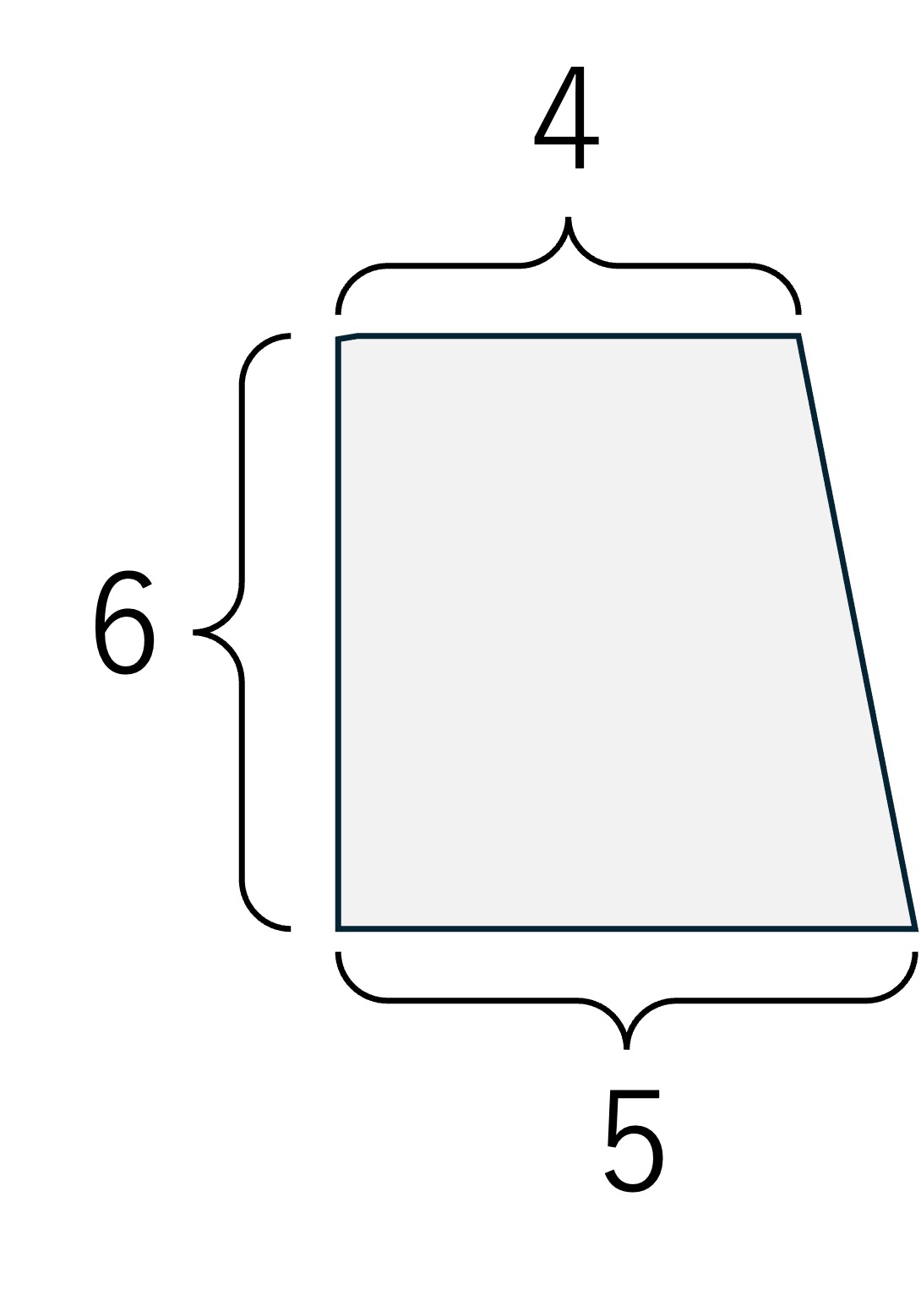
台形の面積計算
上底 4, 下底 5, 高さ 6 の台形の面積の計算は、数式通り入力の関数電卓(演算子の優先順位対応機種)では以下のような操作となる。
( 4 + 5 ) × 6 ÷ 2 =
ここで括弧が必要なのは、当然ながら、 × の優先順位が + より高いためである。だが、これは見方を変えると、「+の優先順位が×より低い」ことを計算を始める前から認識し、それに注意しながら入力を進めなければならないということである。また、関数電卓でない一般の電卓など、機種によっては演算子の優先順位を処理しないものがあり( 4 + 5 × 6 ÷ 2 = という入力で台形の面積が正しく計算できるもの)、電卓を使用する際にそのどちらであるかを認識していなければならない。それに対し、RPN電卓では、以下のように操作する。
4 ENTER 5 + 6 × 2 ÷ RPN(逆ポーランド記法)は演算子の優先順位に関係なく数式の解釈が一意に決定する。各演算子はそれぞれ、それが実行されるタイミングでスタックトップの2つの数値を対象に計算すると決まっているので、当然である。
思うに、これが「電卓にとって」の、RPNの最大のメリットの1つと言えるだろう。各計算ステップでは「どの数値を、どうしたいのか」だけを考えればよく、数式の解釈ルール(優先順位を含む)を気にする必要がないのだ。これらは重箱の隅をつつく議論のように思われるかもしれないが、「あ、括弧を入れ忘れた・・」のような小トラブルは思考の中断を招く。RPN電卓ではそのようなトラブルが起こらず、計算に集中できる。
さらにこの問題を深堀りすると、「演算子の優先順位とは?」という疑問に行き着く。数式解釈において、加減算より乗除算の優先順位が高い、と決められているのは、「積和演算」「多項式」に代表されるように、「そのように計算する場合が多い」ということに過ぎない。しかし上の台形の面積計算のように、常にそうだとは限らないのである。そもそも、我々には「どう計算したいのか」という概念が先にある。数式はその計算手順の1つの表現に過ぎず、計算そのものにとっては必ずしも必要ではない。「演算子の優先順位」問題は中置記法を使用する場合にだけ現れる、必要悪なのである。逆ポーランド記法とRPN電卓は、この優先順位というノイズに邪魔されることがない。
中間結果を確認、保存しながら計算できる
ここでは少し具体的に、以下の回路のLEDに流れる電流値を求めてみよう。
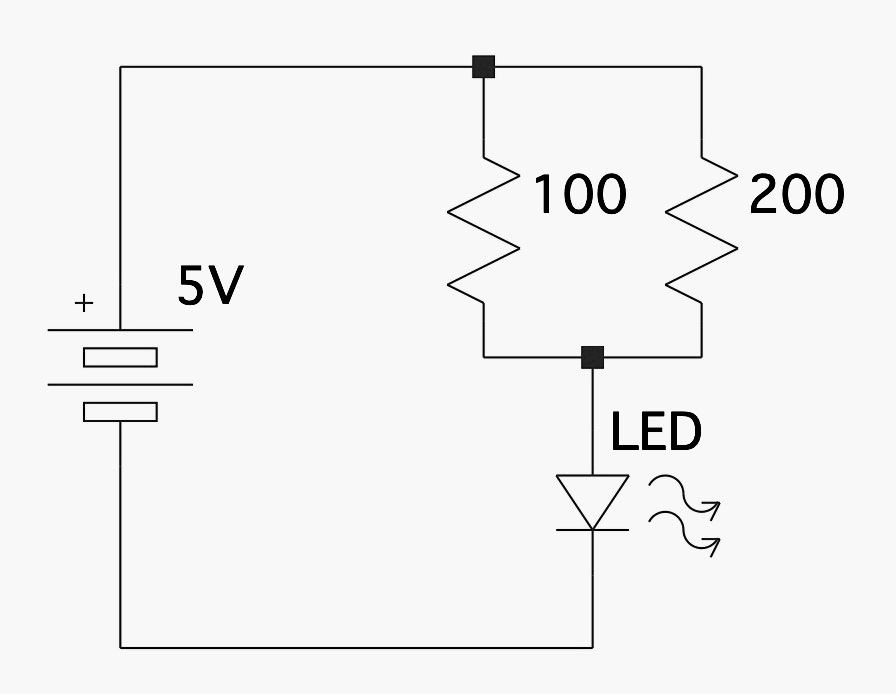
LEDを点灯させる回路の例
まずこの回路を見ると、抵抗器が並列になっているところが厄介だなと感じる。まずはここの合成抵抗を求めてしまおう。 数式ではこの合成抵抗は以下の数式、
| \[ \frac{1}{\frac{1}{100}+\frac{1}{200}} \] |
で計算されるが、RPN電卓では以下のように操作する方が多いだろう。
100 INV 200 INV + INV
ここでINVは逆数を求める単項演算子で、電卓のボタンでは1/xと表記されることが多い。これにより結果は 66.6667 Ω と求まる。電気のことを少しわかっていれば、この結果が100Ωより少し小さい値となっていることから正しく合成抵抗が計算されていることを(無意識に)確認するだろう。そもそも、この並列の合成抵抗の計算そのものが数式通り入力の電卓では厄介だ。 1 / から入力を始めなくてはならず、分母から計算を始めることが出来ない。括弧の入力も必要だ。機種によっては計算結果に対してキー一発で逆数が求められる電卓もあるが、それはまさに「RPN電卓の良さ」を取り入れた機能と言える。そう、結局、電卓を便利にしようとすると、その操作はRPNに近づいていくのだ。
次に電流値を求めるが、このときにLEDの順方向電圧降下を考慮する必要がある。順方向電圧降下はLEDの種類によって異なるので、いったんこの合成抵抗値のバックアップを取っておこう。これには単にENTERを押せば良く、スタックトップが複製され、スタックには 66.6667 が2つ並ぶ。
まずLEDの順方向電圧降下として、赤色LEDで一般的な 2 V で計算してみよう。電源電圧が5Vなので、以下の操作で抵抗器に掛かる電圧を求める。
5 ENTER 2 - すると結果は 3 V となり、スタックは
66.666766.66673
|
のようになっているはずである。
最後にいよいよ、電流値を求める。オームの法則は$IR=V$なので、電流値は$I=V/R$で求められる。ここで少し、その数式の変形(移項)に気を取られることがあるかもしれない。しかし、RPNでは数値がスタックに残っているので、焦らずゆっくり、そのことだけを考えれば良い。そして、スタックにVとRが逆に積まれていることに気づくので、SWAPでこれらの2つを入れ替えて計算する。
SWAP /すると結果的に、以下のように求めたい電流値45mA(0.045)が得られる。
66.66670.045
|
では白色LEDではどうだろうか。白色LEDの順方向電圧降下を3.2Vとすると、計算過程は以下のようになる。DROPでスタックトップの0.045を捨ててもよいが、ここではSWAPでスタックトップの2つを入れ替えて保存しておくことにした。
SWAP 5 ENTER 3.2 - SWAP /
結果、以下のように電流値27mA(0.027)が得られる。操作としては最後にSWAP /をするかわりに/ INVとする、つまり割ってしまってから逆数をとる手順でも良い。
0.0450.027
|
別の方法でも計算できる。LEDの順方向電圧降下を電流によらず一定値と考えると、まず
5 ENTER 3.2 -ENTERで複製し、次にそれぞれの抵抗器に流れる電流を求める。数式でいうと$\frac{5 - 3.2}{100} + \frac{5 - 3.2}{200}$の計算を行うわけだが、最初のENTERで分子の値を複製して再利用している。
ENTER 100 / SWAP 200 / ++を押す直前のスタックの状態は以下のようになっている。
0.0180.09
|
これは各抵抗器に流れる電流値であり、これを確認しつつ、最後に+を押すことで、やはり27mA(0.027)が得られる。ここからさらに、各電流値にLEDの順方向電圧値をかけ、それぞれのLEDの消費電力がほぼ同じであることを確かめるのも簡単である(具体例は省略する)。
このようにRPN電卓では、中間結果を細かく確認しながら計算を進めることができる。前述したように計算結果の再利用も容易で、それをこまごまと行える点に美点がある。「100円のりんごを7個、150円の梨を6個、120円のシュークリームを・・」のような積和演算も、各小計をスタックに積んで1つずつ確認しながら、最後にそれらの和を取るようなことができるわけである。
以上、やや長くなったが、RPNでの試行錯誤的な計算のメリットがいくらか伝わったであろうか。事前に数式を組み立てなくても、各要素を順に計算していき、それらの結果を組み合わせて目的の値を求めることができる。言い換えれば、最終目的に必要な数字を部品として揃え、ボトムアップ的に組み立てていく・・という過程になじみやすい。また、計算結果をスタックに複製しておくことも簡単で、異なる条件での計算も容易に行える。
通常の電卓でも、計算手順を細かく刻みながら操作すれば、中間結果を確認しながら計算できる・・と思われるだろう。しかし前述のように、数式通り入力の電卓では計算結果の再利用に制限があったり、操作ミスで失われたりしがちなので、ちょっとややこしい計算になると「一気に数式を入れて計算する」ということになり、ボトムアップに、試行錯誤的に計算をしていく方法になりにくい。
アンドゥ機能との親和性が高い
RPN電卓はアンドゥ(取り消し)機能との親和性が高い。数式通り入力の電卓でもアンドゥ機能を備えたものはあるが、RPN電卓では数式入力に比べて計算過程が細切れになりやすく、また各計算段階の状態変化がスタックのみという明快さがあるため、アンドゥ操作がより直感的に行え、その動作が理解しやすい。もとに戻ったスタックの値を見ることで、どの段階まで戻ったのかを把握することも簡単である。
さきの電流計算の例では異なる種類のLEDに流れる電流を求めるために、合成抵抗を求めたところでENTERを押して値の複製を行ったが、これをせずとも、アンドゥ機能でそこまで戻れば良い。電源電圧が変わった場合なども同様である。
私は高校生時代(1988年ごろ)に、当時の自分としてはかなり奮発してHP-28Sを購入した(定価47,000円だった)。この電卓では数式処理(数式の因数分解や微積分など)が可能だったり、すべての関数が複素数に対応していたりと($\sin(\sqrt{-1})$のような計算が可能で、結果の複素数や数式・行列など、どんなものでもスタックに積める)、あらゆる点で驚異的な電卓であったが、日頃の計算でもっとも重宝したのがアンドゥ機能であった。試行錯誤を伴う電卓にはアンドゥ機能が不可欠であり、RPN電卓はその実装面でも、操作性の面でも親和性が高い。私自身も自作のRPN電卓(例:ウェブアプリ版)には原則、多段階のアンドゥ機能を備えている。
おわりに
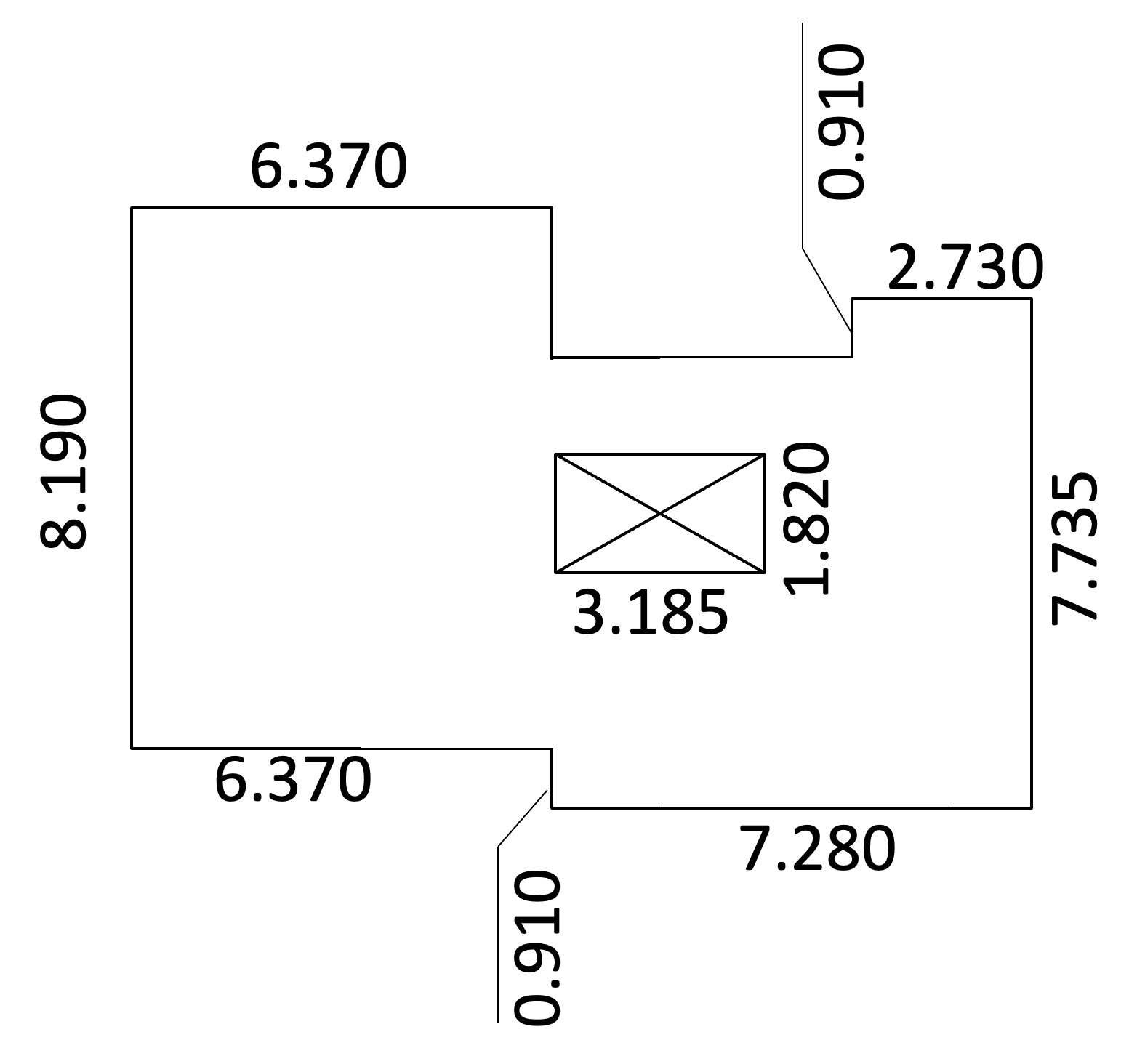
とある建物の二階の平面図。
実線で囲まれた部分から、☒で示す吹き抜けを引いた面積を計算する
最後にもう1つ、簡単な例を示そう。上の平面図から登記上の床面積を求めたいとき、この計算を通常の電卓で行うのはちょっと面倒だ。なぜなら、長方形に分割したときの辺の長さを差で求める必要があり、メモをとりながら計算したくなるのではないだろうか。しかし、RPN電卓ならそんなことをせずとも、たやすく計算できる。答えは98.5439になるので、ウェブアプリ版のRPN電卓などを用いて、計算に挑戦してみて欲しい。
これまでに述べた、通常の電卓での「困りごと」には、それぞれ個別の機能で解決が図られているものもある。アンサーメモリー機能や積算機能、さらにはドットマトリクスディスプレイによる美麗な数式表示やヘルプ、マニュアル表示などである。しかしRPN電卓が優れているのは、たった一つの「逆ポーランド記法」というフレームワークで、これらの困りごとを一挙解決している点にある。RPNの利点として、電卓の実装(プログラミング)が簡単であることも挙げられるが、これはなにも制作者側のメリットだけではない。プログラムが簡単である、ということは、その動作がシンプルで理解しやすい、ということにも直結しているのである。
以上、RPN電卓の良さについて説明してきた。RPN電卓は決して難しいものではなく、むしろ計算をシンプルにし、計算に集中できる道具であることがお分かりいただけたであろうか。確かに普通の電卓に比べると若干の慣れを要するが、そのハードルは決して高くなく、一度馴染んでしまうと、とても快適な世界が待っている。