究極の電気用計算尺 Pickett N16-ES

Pickett はアメリカの計算尺メーカで,N600-ES というポケット計算尺が非常用としてアポロ計画で使用され月へ行ったことで有名である.また Pickett の多くの計算尺は全金属製(アルミ製)で高湿度環境に強く,また様々な用途に応じて専用設計された特殊計算尺も多く製造している.ここで紹介するのは,電気設計技術者向けの高機能計算尺,N16-ES である.
電気設計用尺度の使い方
Pickett N16-ES の詳しい使い方は,海外サイトで公開されている添付マニュアル等を読めばよいが,英語しかなく,またあまりわかりやすいとはいえない.そこでここではごく簡単にその使い方を紹介する.
まずそれぞれの尺度の意味は以下のようになっている.

これらの尺度の基本的な機能は大きく2つに分類される.1つ目はコンデンサとコイルのリアクタンス(コイルやコンデンサに流れる交流電流に対する電圧の比)の計算である.リアクタンスは交流信号の周波数によって変化するので,尺度 F(または各周波数 ω)を中央の↓に合わせる.すると,尺度 C に設定したコンデンサの静電容量に対する容量性リアクタンス(Xc = 1/(2πfC) または Xc = 1/(ωC))が,その値に対向する尺度 Xc で直読できる.尺度 L(尺度 C と共用)にインダクタンスをセットすれば,誘導性リアクタンス(XL = 2πfL または ωL)が尺度 XL で直読できる.滑尺とカーソルをセンターに合わせた状態で言うと,1Hz, 1F の容量性リアクタンスは 0.159Ω (1/2π), 1Hz, 1H の誘導性リアクタンスは 6.28Ω (2π) と読めることになる.当然,100kHz, 1μF の容量性リアクタンスは 1.59Ωであると読んでもよい[*1].電気回路では,この位取りの範囲が大きいことが問題になるが,これは他の補助尺度で計算できる.これについてはのちに述べる.
2つ目の機能は共振周波数の計算である.コイル L とコンデンサ C による共振回路の共振周波数は 1/(2π√LC) である.平方根を処理するため,共振周波数の計算のためには L or C よりも倍の密度で刻まれた Cr / Lr の2つの尺度が別途設けられている.5μH のコイルと 0.505μFのコイルの共振周波数は 100kHz であるが,中央のカーソル部分には1が現れている[*2].この位取りはやはり,補助尺度を用いて別に処理する.
滑尺に刻まれた F, λ, ω, τ は一定の関係(λ=300000000/F, ω=2πF, τ=1/ω)があるため互いの換算に利用できる.また詳細は割愛するが,LCR交流回路では誘導性・容量性リアクタンス(インピーダンス)を虚部,抵抗成分(レジスタンス)を実部としたときの偏角により位相の遅れや進みが求められる.そこでθの尺度では,実部と虚部の比から位相を求めることが出来る.つまり尺度θは,通常の計算尺のT尺(tan尺)と同じであるが,Xc, XL尺が右端から左端まで100倍の尺である(通常の計算尺のA/B尺のようになっている)ことから,中央から左右対称のような目盛りが刻まれている.1:1 から 1:10 までは下側(45°〜5.7°),1:10 から 1:100 までは上側(5.7°〜0.6°)を用いる.
実部と虚部の比からDまたはQ値を求めることもでき,それを直接 dB に変換することも出来る.最下部のcosθは,電流値の絶対値を求めたい時に用いるものであろう.位相遅れ・進み角のコサインでレジスタンスを割ればインピーダンスの絶対値が求められるが,電流値を求めるには再び逆数を求めることになるので,cosの値が直読できるのが便利なのだと思われる.最上部のθ尺度下部(5.7°〜84.3°の範囲)からcosθが直読できる.

さて,位取りのための補助尺度であるが,これは下部に5種類が刻まれている.先に述べた共振周波数の例*2では,それぞれの補助単位の指数部(μH, μFなのでともに -6)を L'R と C'R から選び,縦に揃える(赤丸部分).すると,計算尺の右端のブリッジ内側に対応する周波数の指数部(青丸部分,-5)が現れる.これを F の尺に現れた 1 とかけることで100kHz となるわけである.また同様にリアクタンスの計算例*1でも,周波数が100kHz(青丸部分),静電容量の補助単位がμFであるため,C' の尺度(青線部分)を読むと,X'c は 1 となるため,100kHz, 1μFのリアクタンスは 0.159 * 10 = 1.59Ωと計算されるわけである.
三角関数を用いたピタゴラスの定理の計算
この Pickett N16-ES では,表側の三角関数の尺度が通常とは異なり,左右逆向きに置かれている.つまり普通の計算尺では,S, T, ST などの尺度の角度値と C / D 尺の値とが対応するが,この計算尺ではかわりに CI 尺を用いる.これによって最小限の操作で三角関数を用いたピタゴラスの定理の計算(直角三角形の2辺から,他の1辺の長さを求める計算)が容易にできる.
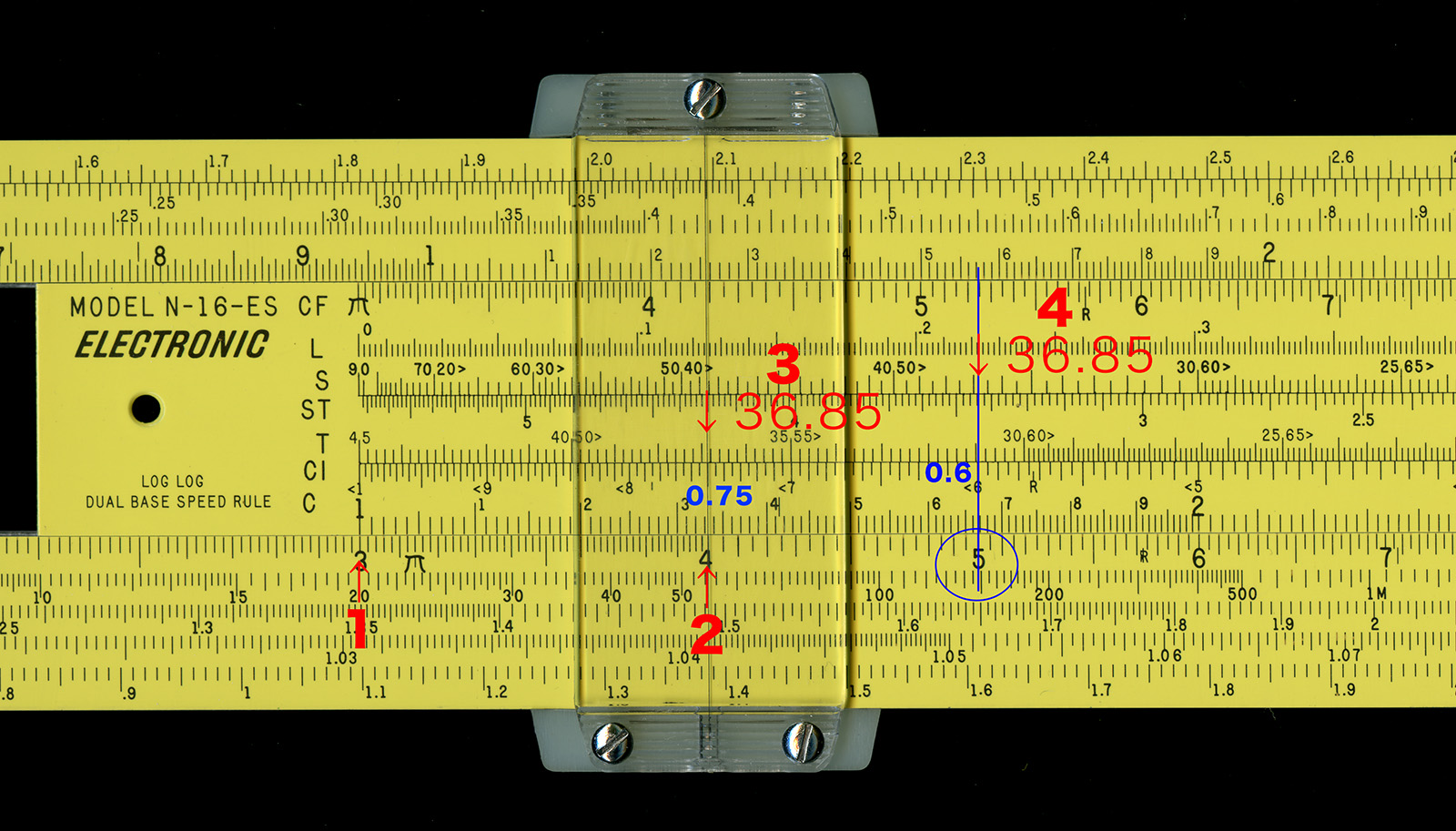
まずは有名な,辺の長さが 3・4・5 の直角三角形の斜辺の長さを求める操作をしてみよう.まずは滑尺を動かし,短い方の辺 3 のところに滑尺の基線 1 を合わせる.そうして次に D 尺の4のところをみると,CI尺では 3/4 = 0.75 の値が得られる.これに対応するT尺の角度は,長さ3の辺の対角(この直角三角形で最も小さい角)の角度であり,36.85 と読める(tan(36.85) = 3/4).この値を次に S 尺上で取ると,sin(36.85) = 0.6 が CI 尺で得られる.この値 0.6 で,接する辺の長さ 3 を割ると斜辺の長さ 5 が得られるので,D尺上で値 5 が直読できる.ここでも再び,CI 尺とC尺が逆数の関係になっていることが利用されるわけである.
このような斜辺の長さの計算は複素数の絶対値の計算で多用され,これは複素インピーダンスを用いて電流値と電圧値の関係を求めるのに利用される.そのため,この電気尺 N16-ES では三角関数が逆尺になっているのである.
この計算尺のその他の特徴として,L尺(log C)の他に Ln尺(ln C,つまり自然対数)が備わっている点も面白い.また三角関数関連では,P 尺(ピタゴレリアン尺)が存在しないが,裏面に cos θ があるため大きな不自由はなく,また一手間増えるが,三角関数を用いた計算も可能である.双曲線関数(SH, TH) はあまり使用されることが無いため,この部分にLL01〜LL03 があっても良かったと思うほかは,なかなか良く出来た計算尺であるといえる.
その他の特徴
Pickett は米国製の計算尺である.米国製というとどうもアバウトな仕上げを想像してしまうが,なかなかどうして良好な精度と高品質な仕上げの計算尺であるといえる.

Pickett の計算尺にはこのような黄色のものが多く見られる.これは Eye Saver と言われ,目の疲労を抑える色彩であるということである.白に比べて見やすいかどうかというと,個人差があると思われるが,使ってみると特に違和感はなく,確かに明るすぎずに疲れにくいかもしれない.N16-ES のように型番にESが付くものが黄色で,N4-T のように T が付くものは白色仕上げである.
目盛りは黄色の塗装の上に印刷されているようである.印刷というと刻印に比べ精度や耐久性の点で劣るように感じられるが,使用した様子では尺度の目盛りの精度は十二分で,どのようにずらしても合うべきところはピシャリと合う感覚は高い.歪みやすいシルク印刷などでなく,精度の高い印刷法を用いているのであろう.また黄色の基部はつや消しになっていて,つやのある多くの計算尺に比べて使いやすい.ケースは内側にしっかりしたプラスティック製のさやが入っており,金属製の計算尺でもっとも問題になると思われる歪みが起こらないように配慮されている.非常によく出来たケースである.


この計算尺では滑尺の噛み合わせが浅めに作られており,またその形状も台形であるため,動きが非常にスムーズで,自重で滑尺が動くことがない割に静摩擦を感じさせず微調整がしやすく,スムーズな操作ができる.操作感はほかに比べて高い方であると思う.カーソルは樹脂製であるが合理的な作りで材質がよく,スムーズで壊れにくいと思われる.
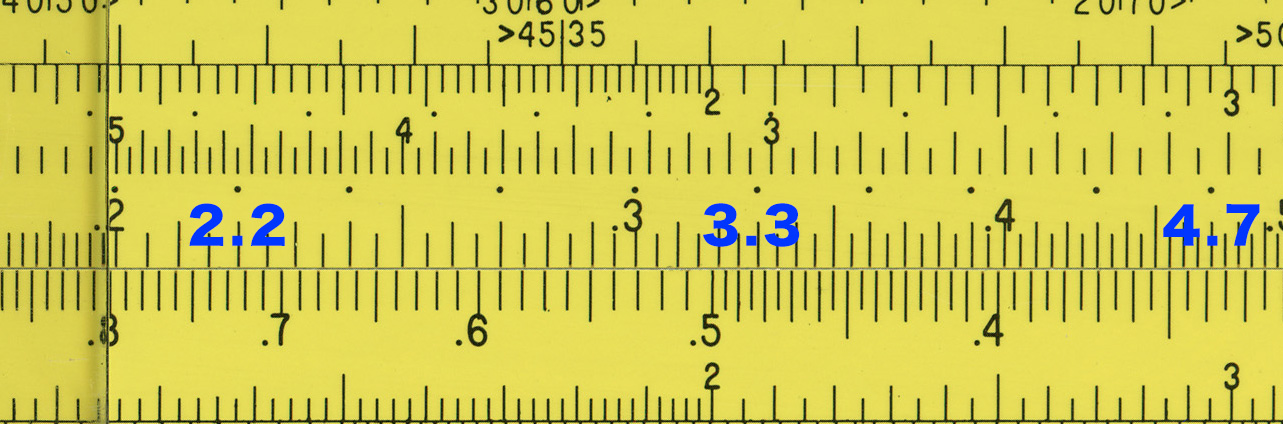
電気技術者向けの心憎い機能として,リアクタンスの目盛りに打たれた付点がある.この付点は電子部品で広く用いられているE24系列(10倍の区間を,等比的に24段階に分けたもの)に対応しており,現れた目盛りをすぐにE24の部品に置き換えたり,E24の部品の値を計算尺にセットするのが簡単となるように工夫されている.上の図は説明のため,E24 のうち特に広く用いられているE6系列の値(4つ飛ばしに現れる)を青字で記入した.







