計算尺の原理と乗除算の方法

計算尺とは対数を利用して乗除算を簡単に計算できるようにしたものである。現在、計算尺に興味を持つのはほぼ理系の方に限られるのではないかと思う。そこでここでは、あえて表層的な説明はせずに対数に基づく計算尺の原理から説明を行う。

計算尺の原理

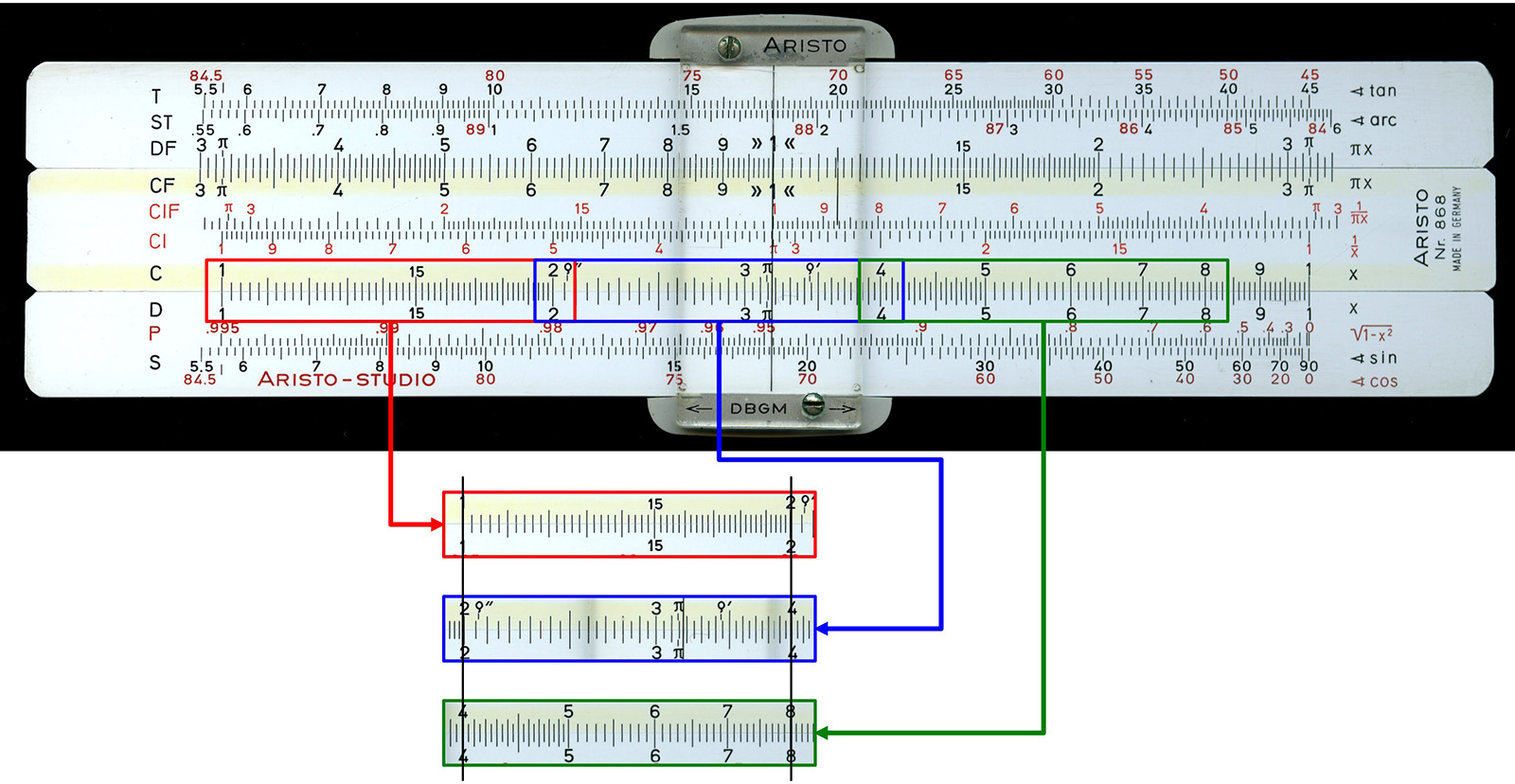
図１　対数目盛における間隔と比の関係

計算尺には様々な目盛り（尺度）が刻まれているが、現在の計算尺で最も中心となる尺度である C/D 尺から説明することにする。C/D 尺は $1$ から $10$ までの範囲の値 $x$ について常用対数 $y = \log(x)$ を求め、その位置 $y$ に値 $x$ を刻んだものとなっている（以降、値を$x$で、またその値が計算尺上に置かれた位置を$y$で表す）。

このようにすると計算尺の上では、同じ比を持つ値同士が等間隔で並ぶ。例えば上の図では、尺度 Dの上で $x = 1$ と $x = 2$ の目盛り（位置）の間隔は、$x = 2$ と $x = 4$ の目盛りの間隔や、$x = 4$ と $x = 8$ の目盛りの間隔と等しくなる。なぜなら $y_2 = \log(x_2)$ と $y_1 = \log(x_1)$ の差（間隔） $y_2 - y_1$ は、$\log(x_2) - \log(x_1) = \log(x_2 / x_1)$ となり、２つの値の比 $x_2 / x_1$ で決まるためである。

図２　固定尺と滑尺の間の比の関係

尺度Cと尺度Dは同じ目盛りが刻まれており、それらの位置関係がずれるようになっている。このずれが比として働くことで乗除算ができる。先に述べたように、上の図で $x_2$ と $x_1$ の比（$x_2 / x_1 = 6 / 3 = 2$）は、 $x_4$ と $x_3$ の比（$x_4 / x_3 = 2 / 1 = 2$）と同じ $2$ となっている。つまり、図２のような関係にある４箇所の値は \[ \frac{x_2}{x_1} = \frac{x_4}{x_3} \] のような関係が保たれる。これらの値 $x_1$ 〜 $x_4$ のうちどれか３つに計算尺上の値をセットすると、残りの変数で乗除算の結果が得られるというわけである。図２では $x_3 = 1$ であるから、$x_2 / x_1 = x_4$ となる。これを整理すると $x_2 = x_1 * x_4$ となり、$x_1$ と $x_4$ の積 ($3 * 2 = 6$) が $x_4$ の下に現れている。

乗除算と分数の計算

図３　掛け算の原理

計算尺による、より直感的な乗除算の解釈はこうだ。計算尺上では対数が用いられているので、目盛りと目盛りの間の間隔は比を表す。上の図で、$a$ は $x = 1$ と $x = 3$ の間の比 $3$ を表し、$b$ は C 尺上で $1$ と $2$ の間の比 $2$ を表すので、長さ $a$ と $b$ を足したところにある値は $3 * 2 = 6$ となるというわけである。このように、計算尺ではずれ量を常に「比率」ととらえる感覚が重要となる。

計算尺を利用する上では、少し別の捉え方をしたほうがわかりやすいこともある。先の図２において、計算尺上の４箇所の値は $x_2 / x_1 = x_4 / x_3$ の関係にあると説明した。この数式を移項すると、次のような数式に変換することが出来る。 \[ \frac{x_3}{x_1} = \frac{x_4}{x_2} \] これは次のように考えると利用しやすい。まず、C尺（滑尺）とD尺（固定尺）の切れ目を分数の水平線だと考え、その線の上にある数値と下にある数値はそれぞれ分子と分母で、これらが常に同じ比率になっているというわけである。

図４　固定尺と滑尺上の値の比率

上の図において、中央部下（カーソル上）の赤丸内は上に $1$, 下に $3$ があるため、計算尺全体で $1/3$ の比率の設定になっていると見ることが出来る。実際に、$2/6$, $3/9$ のような、約分すると $1/3$ になる組み合わせが多数見つかる。さらに上方の CF/DF 尺の上でも同じ関係が保たれる。CF/DF 尺は C/D 尺を$\pi$だけ（計算尺によっては、$\sqrt{10}$ だけ）ずらして配置した尺度であり、ずれと比の関係は C/D 尺と同じであるため、上方赤丸内のように $1/3$ の組み合わせ（固定尺と滑尺の位置関係が逆なので上下反転する）が見つかる。さらにその右では、$5/1.5$ のように読める部分があるが、これは $5/15$ （または $0.5/1.5$）と解釈する。計算尺では $1$ から $10$ の範囲の対数をとり、次の範囲（$10$ から $100$ の範囲）は $1$ から $10$ の範囲を共用している。同様に、$0.1$ から $1$ の範囲も $1$ から $10$ の範囲で取り扱う。つまり位取りは無視され、これは使用者が解決しなければならない。右の青丸の内部は $7/21$ （または $0.7/2.1$）のように読むことになり、他の箇所でも比率が 1:3 になっている目盛りの組み合わせが多数見つかることが分かる。

C/D 尺に対し CF/DF 尺が$\pi$（計算尺によっては$\sqrt{10}$）ずらしてある理由は、固定尺と滑尺がずれることにより値の対向関係が読めなくなること（目外れ）を防ぐためである。図４で、D尺上の $1$ から $3$ の範囲は、C 尺上の対応する値が読み取れない。しかしそのかわりに、DF尺の上では（$3$〜$9$ の範囲が読めない代わりに）$0.9$〜$3$ の範囲を読み取ることが出来る。滑尺を固定尺に対して半分以下しかずらさないように留意すると、このような「目外れ」の影響を受けずにすむ（例えば $1:5$ の比率を求めたいときは、C尺の左端の $1$ を D 尺の $5$ に合わせる代わりに、滑尺を左へ動かし、C尺右端の $1$ をD尺の $5$ に合わせれば良い）。