スピーカーのシミュレーション
ここではスピーカーユニットとエンクロージャを電気回路(等価回路)でシミュレーションする方法を紹介する.力学現象の電気回路による表現
スピーカーや自動車の足回り(サスペンション)などにみられる,力と速度の関係を電気回路に置き換える.
力学現象の数式表現
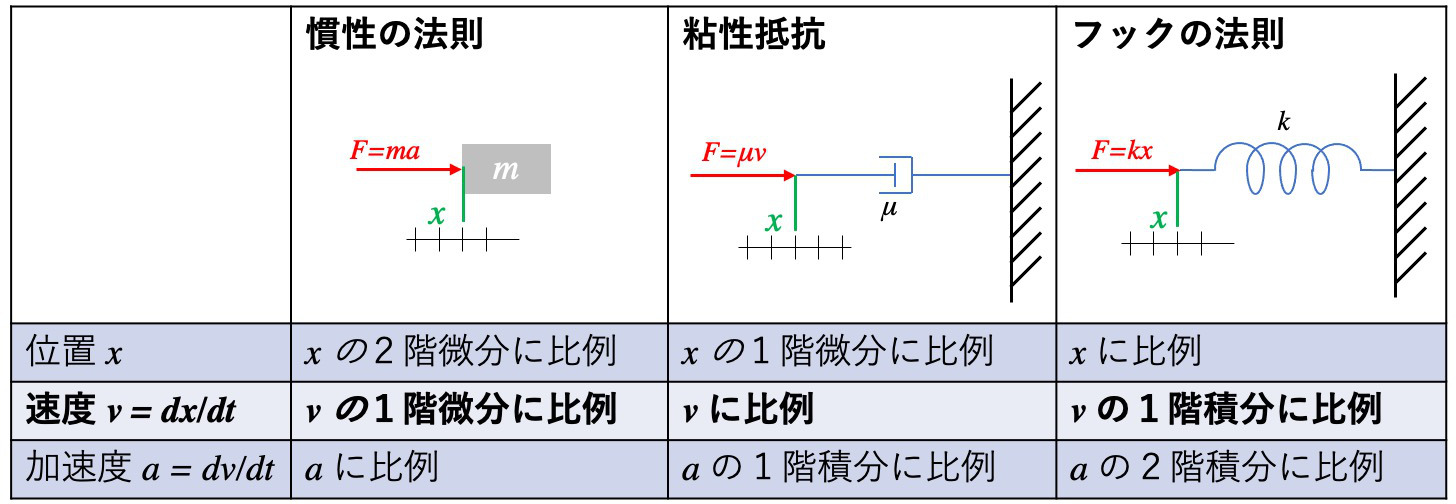
- 慣性の法則
質量 $m [kg]$ の重りに力 $F [N=kg \cdot m/s^2]$ が加えられたときの加速度 $a [m/s^2]$は,以下の慣性の法則で表される. $$F=ma = m \frac{dv}{dt}$$ - 粘性抵抗
抵抗には摩擦や空気抵抗などいろいろな現象があるが,ここでは速度が遅いときの気体や流体による粘性抵抗を扱う.この抵抗力 $F$ は,粘性抵抗$\mu[N \cdot s/m=Kg/s]$ と物体の速度 $v[m/s]$から以下のように表される. $$F=\mu v$$ - フックの法則
ばね定数 $k [N/m]$ のばねに $F$ の力が加えられたときの,ばねの変位 $x [m]$は,以下のフックの法則で表される. $$F=kx = k \int v dt$$ $$v = \frac{1}{k} \frac{dF}{dt}$$
電気回路の数式表現
電気回路に用いられるコンデンサ・抵抗・コイルでは,電圧$V$と電流$i$の間の関係は以下のように表される.- コンデンサ
コンデンサに流れる電流 $i [A]$ は,両端の電位差 $V [V]$ と静電容量 $C [F]$ から以下のように表される. $$Q = \int i dt = C V$$ $$i = C \frac{dV}{dt} $$ - 抵抗(オームの法則)
抵抗の両端の電位差 $V$ は,電流 $i$ と電気抵抗 $R [Ω]$ から以下のように表される. $$iR = V$$ - コイル
コイルに流れる電流 $i$ は,両端の電位差 $V$ とインダクタンス $L [H]$ から以下のように表される. $$V = L \frac{di}{dt}$$
力学現象と電気回路の対応付け
以上のように,力学現象も電気回路も,ある変数が他方の変数に対して積分・比例・微分の関係になっている.微分の反対が積分なので,これらを対応付けには以下の2種類があり,どちらを用いてもよい.力学・電気とも,各法則は係数などがかからない単純な数式で表されているので,単位間も直接,m, kg, N, A, V, F, H などを対応付ければよく簡単である.- 力$F$に電流$i$を,速度$v$に電圧$V$を割り当てる方法(力-電流アナロジ) このとき,慣性の法則にはコンデンサが,フックの法則にはコイルが対応付けられ,$C=m, R = \frac{1}{\mu}, L=\frac{1}{k}$の関係となる.コイルがバネっぽい形だとか,変位と関係のある速度に電位が対応付けられるとか,直感的にはこちらがわかりやすいかもしれない.
- 力$F$に電圧$V$を,速度$v$に電流$i$を割り当てる方法(力-電圧アナロジ) 慣性の法則にはコイルが,フックの法則にはコンデンサが対応付けられ,$L = m, R = \mu, C = \frac{1}{k}$の関係となる.コイルに流れる電流が慣性を持つ感じは,これはこれでわかりやすい.
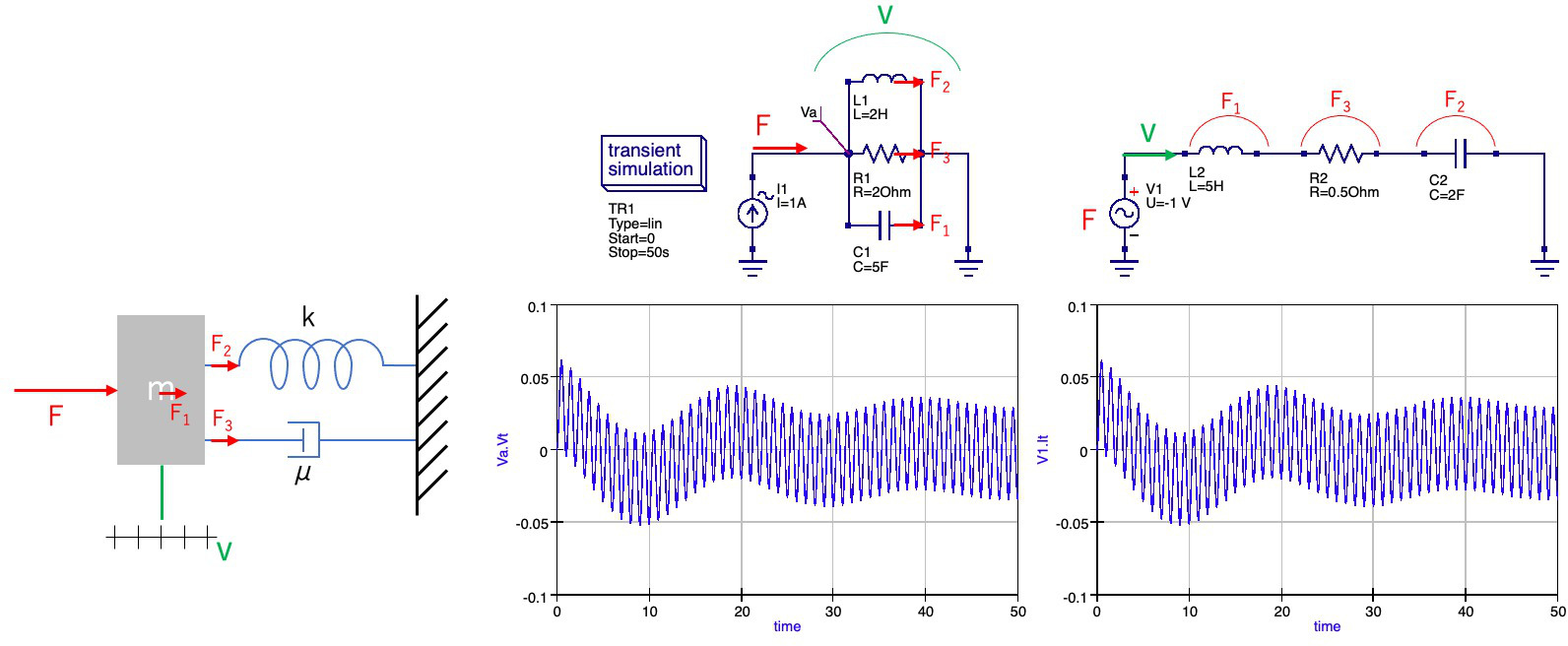
このような対応付けを用いて,重り・バネ・ダンパーからなる系(減衰振動する)を電気回路で表した.重り $m$ には力 $F$ がかかり,これは重りそのものを加速するほかに,バネやダンパーにも伝わり,それらの合力が $F$ となる.1つ目の電気回路ではそれを並列回路で表しており,$F$ に対応する電流がコイル・抵抗・コンデンサに分流する.それらの両端の電位は共通で,これは重りの速度に対応する.2つ目の回路では,分力はそれぞれの素子の両端電圧(分圧)で表され,重りの速度はすべての素子に共通の電流に対応する.いずれも同じ力学モデルを表しているので,シミュレーション結果も当然同じになる.
| 力学 | 力-電流アナロジ | 力-電圧アナロジ |
|---|---|---|
| 力 $F$ | 電流 $i$ | 電圧 $V$ |
| 速度 $v$ | 電圧 $V$ | 電流 $i$ |
| 質量 $m$ | キャパシタンス $C$ | インダクタンス $L$ |
| 慣性の法則 $F=ma = m \frac{dv}{dt}$ | コンデンサ $i = C\frac{dV}{dt}$ | コイル $V = L\frac{di}{dt}$ |
| 粘性抵抗 $\mu$ | コンダクタンス(抵抗の逆数) $R^{-1}$ | レジスタンス(抵抗) $R$ |
| 粘性抵抗 $F=\mu v$ | 抵抗 $i = \frac{1}{R}V$ | 抵抗 $V = R i $ |
| バネ $m$ | 逆インダクタンス $L^{-1}$ | 逆キャパシタンス $C^{-1}$ |
| フックの法則 $F= kx = k \int v dt$ | コイル $i = \frac{1}{L} \int V dt$ | コンデンサ $V = \frac{1}{C} \int i dt$ |
| 分力 | 分流(並列回路) | 分圧(直列回路) |
スピーカの等価回路
スピーカユニットの力学的な動きを電気回路で表現する.次に,アンプからの電力がスピーカを動かす部分と,エンクロージャ内部の空気の動きを回路に付け加えることで,スピーカ全体を電気回路で表現する.可動部分の等価回路
スピーカユニットは振動板(コーン)やコイルが,その周囲のダンパーやエッジで筐体と接続されている.またこれらのダンパー・エッジやコーンは,振動エネルギーが減衰するような材質(内部損失が大きいという)で作られていることが多い.よってスピーカユニットは先に出たバネ・ダンパー・質量系と同じ力学モデルで表すことができる.スピーカユニットを電気回路で表すには,それらの物理パラメータ(質量やばね定数など)を知る必要があるが,それらはたいてい,スピーカユニットのスペックシートに明記されている.例えば以下の数値は,1個 2,000円程度で販売されている Tymphany 社 Peerless PLS-P830985 の仕様(一部)である.
| スペックシート上の表記 | 和訳 | 記号 | 値 |
|---|---|---|---|
| Moving Mass | 運動質量 | Mms | 1.9g |
| Suspension Compliance | サスペンションのコンプライアンス(ばね定数の逆数) | Cms | 963μm/N |
| Mechanical Q Factor | 機械的Q値 | Qms | 4.08 |
| Electrical Q Fqctor | 電気的Q値 | Qes | 0.75 |
| Total Q Factor | 総合Q値 | Qts | 0.63 |
| Resonant Frequency | 共振周波数 | Fs, F0 | 117.16Hz |
| DC Resistance | 直流抵抗 | Revc | 3.63Ω |
| Voice Coil Inductance | ボイスコイルのインダクタンス | Le, Levc | 0.03mH |
| Motor Force Factor | モーターのフォースファクタ | BL | 2.61 Tesla m |
| Effective Piston Area | 有効ピストン面積 | Sd | 21.2cm2 |
| Effective Volume | 等価容積 | Vas | 0.61L |
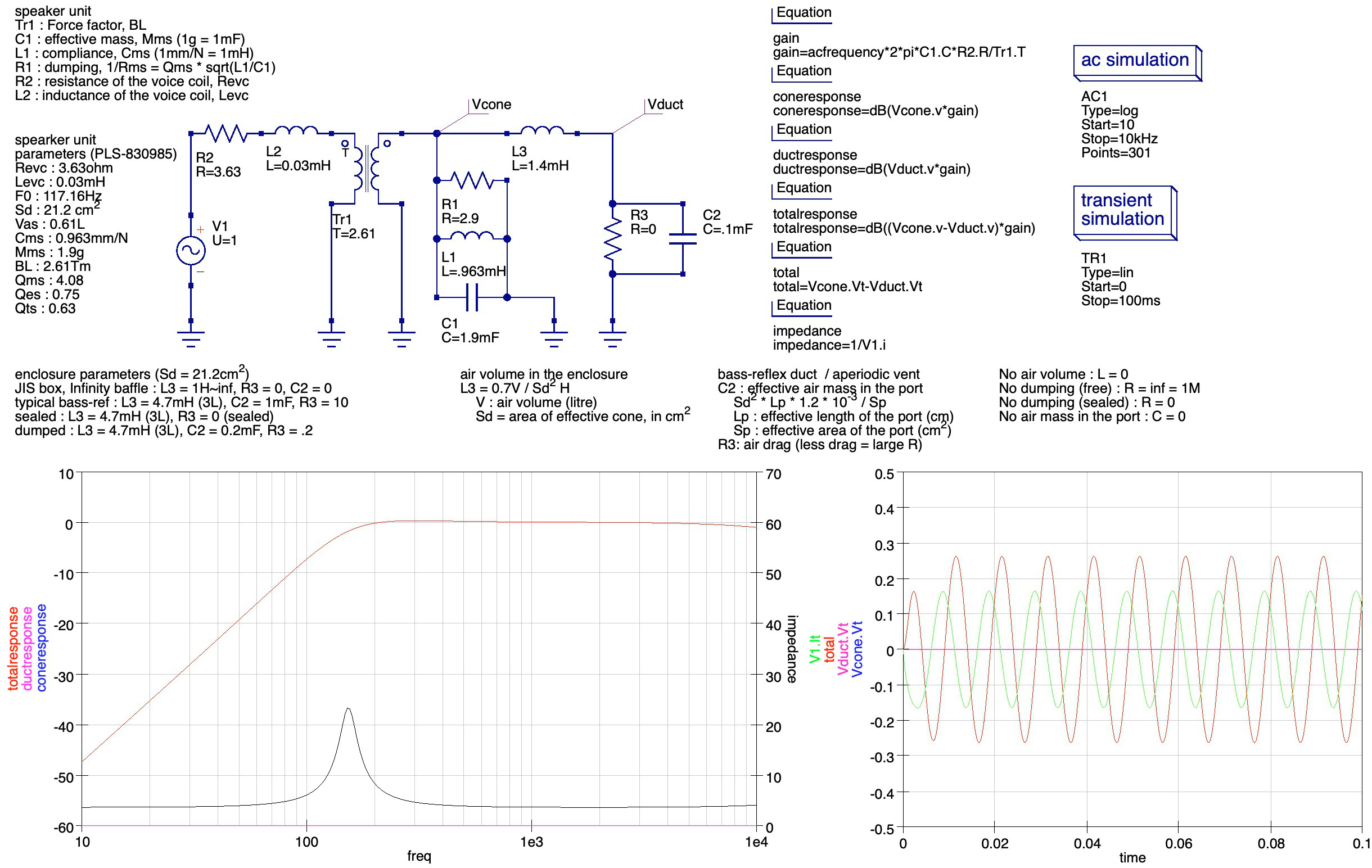
これらを用いてスピーカーユニットの等価回路を以下のように作成した(回路シミュレーションには Qucs を使用した).
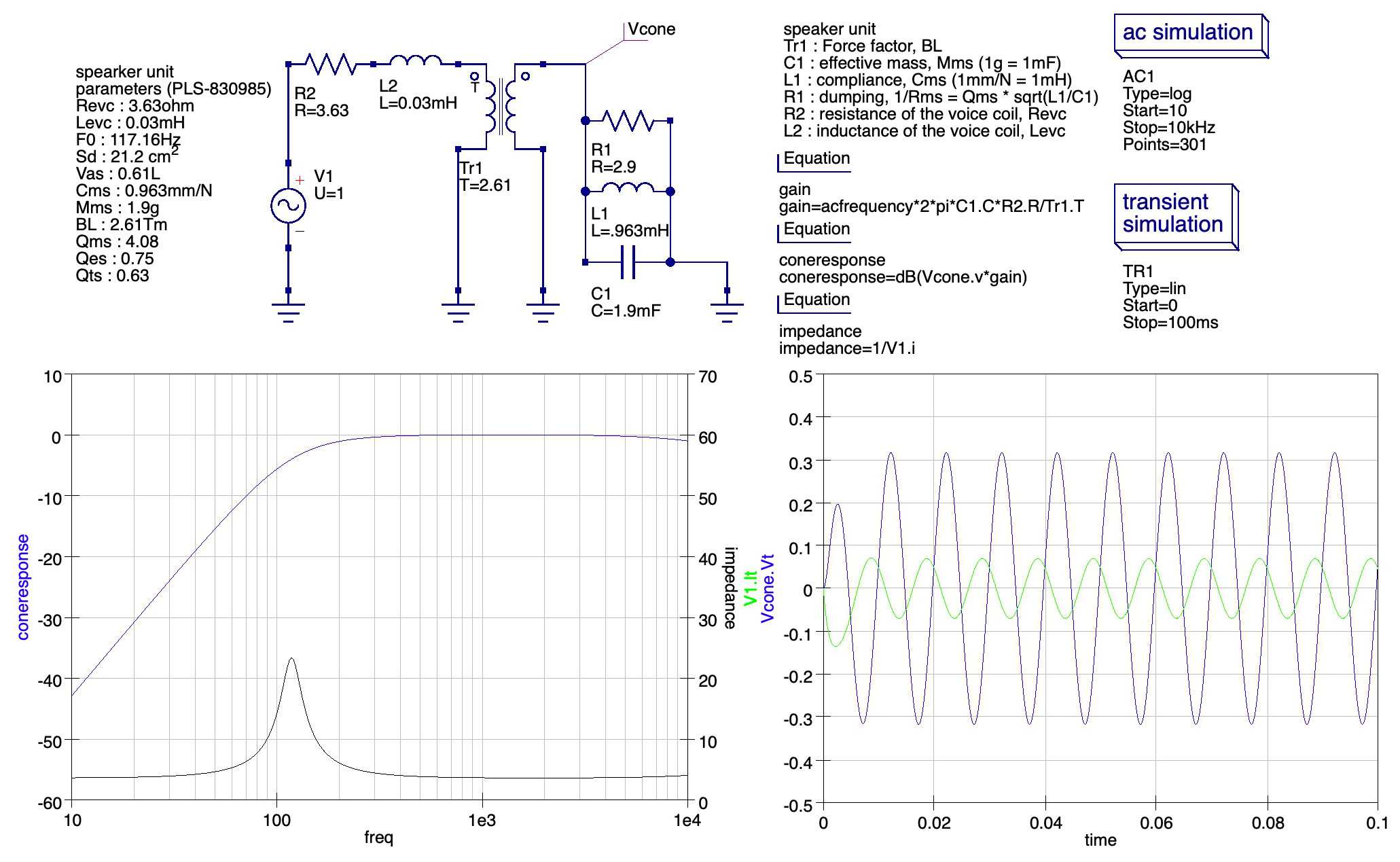
この等価回路では力-電流アナロジを利用しており,スピーカユニットの力学モデルは回路右のLCR並列共振回路である.質量 $Mms$ はコンデンサ C1 で表現されている.スペックシート上で$Mms$と表記されている場合はスピーカユニットの可動部分の質量に加え,コーン紙に押されて動く空気の質量も含まれているので,この値をそのまま C1 に設定すればよい.L1 も $Cms$ の値がそのままセットされている.問題は R1 で,これに相当する値は公開されていない場合が多い.この場合は機械的Q値 $Qms$ を用いて計算する.Q値とは,振動がどれだけ収束しやすいかを表している.摩擦のない振り子は長く振れ続けることになり,これはQ値が高いことを意味する.同じ振り子を水につけると抵抗が増えて(Q値が減少して),振り子の動きはすぐに止まる.並列LCR共振回路のQ値は $Q = R \sqrt{\frac{C}{L}}$で表されるので,抵抗 R1 は機械的Q値 Qms から $R = Q_{ms} \sqrt{\frac{L}{C}}$と計算できる.
電磁気的特性の統合
つぎに,これをアンプと接続する.そのときに,スピーカユニット後部のドライバ部分(ボイスコイルと永久磁石)の特性が問題になる.この部分では流れた電流に比例した力が発生し,また,ボイスコイルの速度に比例した逆起電力が発生するため,現実に力学系と電気回路の間を取り持つ部分と言える.しかし磁石の強さや巻線の長さによってその変換係数が変わり,それはフォースファクタ BL により表される.ここではフォースファクタを,トランス(交流について,電力値(電流と電圧の積)を保ったまま,電流と電圧の比率を変化させる素子)により表現している.また,ボイスコイルは電線が巻かれたものなので電子回路素子のコイルと同じ特性(インダクタンス)を持ち,また電線の電気抵抗もあるので,これらの値 Le (Levc) と Revc をそのまま L2 と R2 にセットすることで等価回路が完成する.スピーカのインピーダンス(印加される交流電圧と交流電流の比)はスピーカの共振状態によって変化する.たとえばブランコを漕ぐとき,ブランコが持つ周期で振れるには僅かな力をタイミング良く加えるだけでよいが,別の周期で振るには大きな力が必要である.つまり共振周波数で振れているときには力(=電流)を要さないため,電圧に対して電流が小さくなる,つまり,抵抗値が大きくなる.左下のグラフ下部の黒線はインピーダンスの周波数による変化を表しており,スピーカユニットのスペックシートにある通りに 117Hz で共振していることがわかる(なお LCR並列共振回路の共振周波数は $\frac{1}{2 \pi \sqrt{LC}}$で表され,また,質量バネ系の共振周波数は $\frac{1}{2 \pi} \sqrt{\frac{k}{m}}$で表される).
なお音圧はコーンの速度の微分に比例するが,この回路は線形回路なので周波数を掛けて計算している.
スピーカのシミュレーション
いよいよエンクロージャ部分の物理特性を組み合わせてスピーカ全体のシミュレーションを行う.代表的な密閉型とバスレフ型エンクロージャの物理モデルは下の図のようになる.
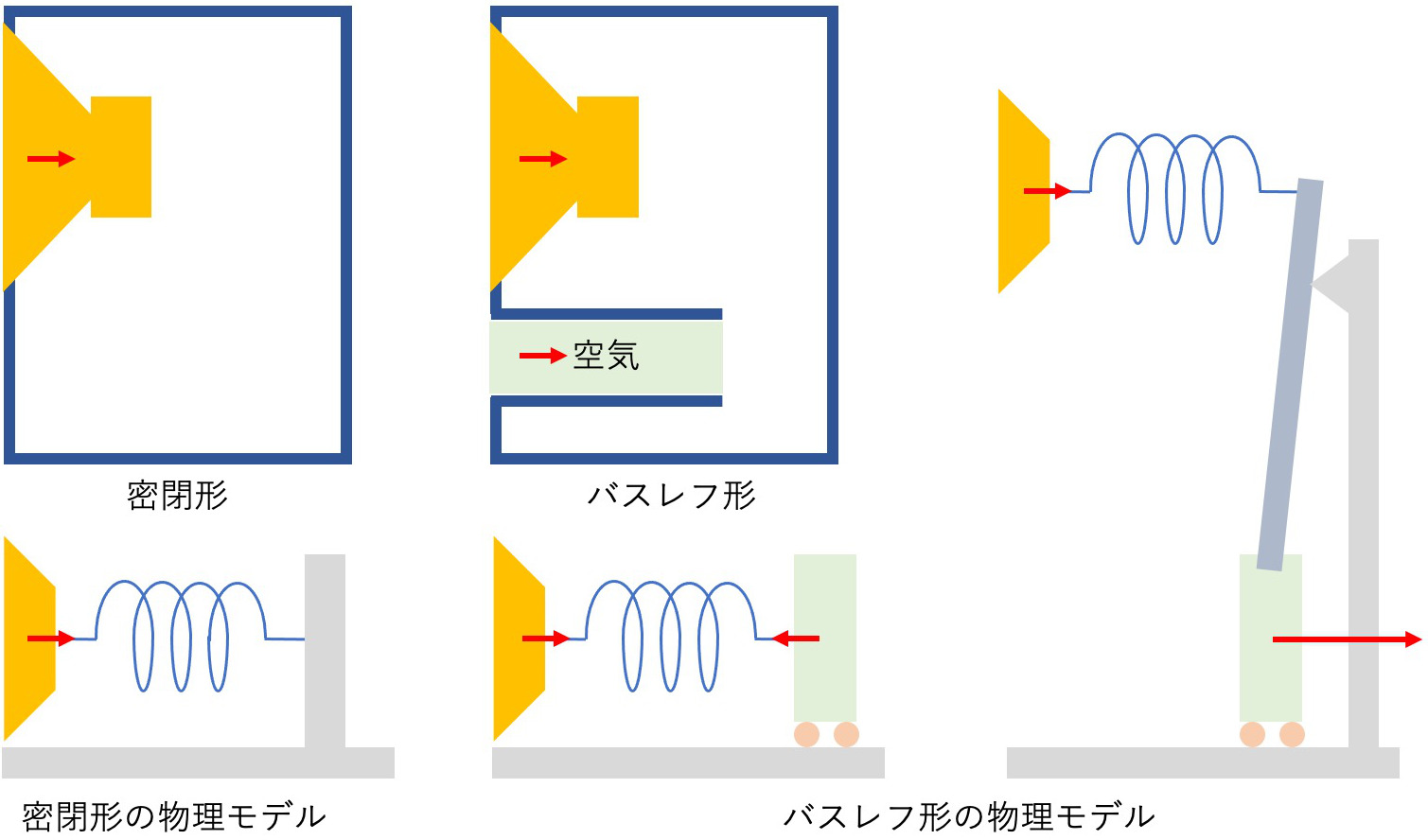
スピーカは,コーンが下がったときに前面は負圧に,背面は正圧になる.背面の圧力が手前に回り込むと打ち消し合って音が聞こえなくなる(特に低音で顕著になる)ので,何らかの板や箱にスピーカユニットを取り付けて,背面の圧力が手前へ回り込みにくくする.
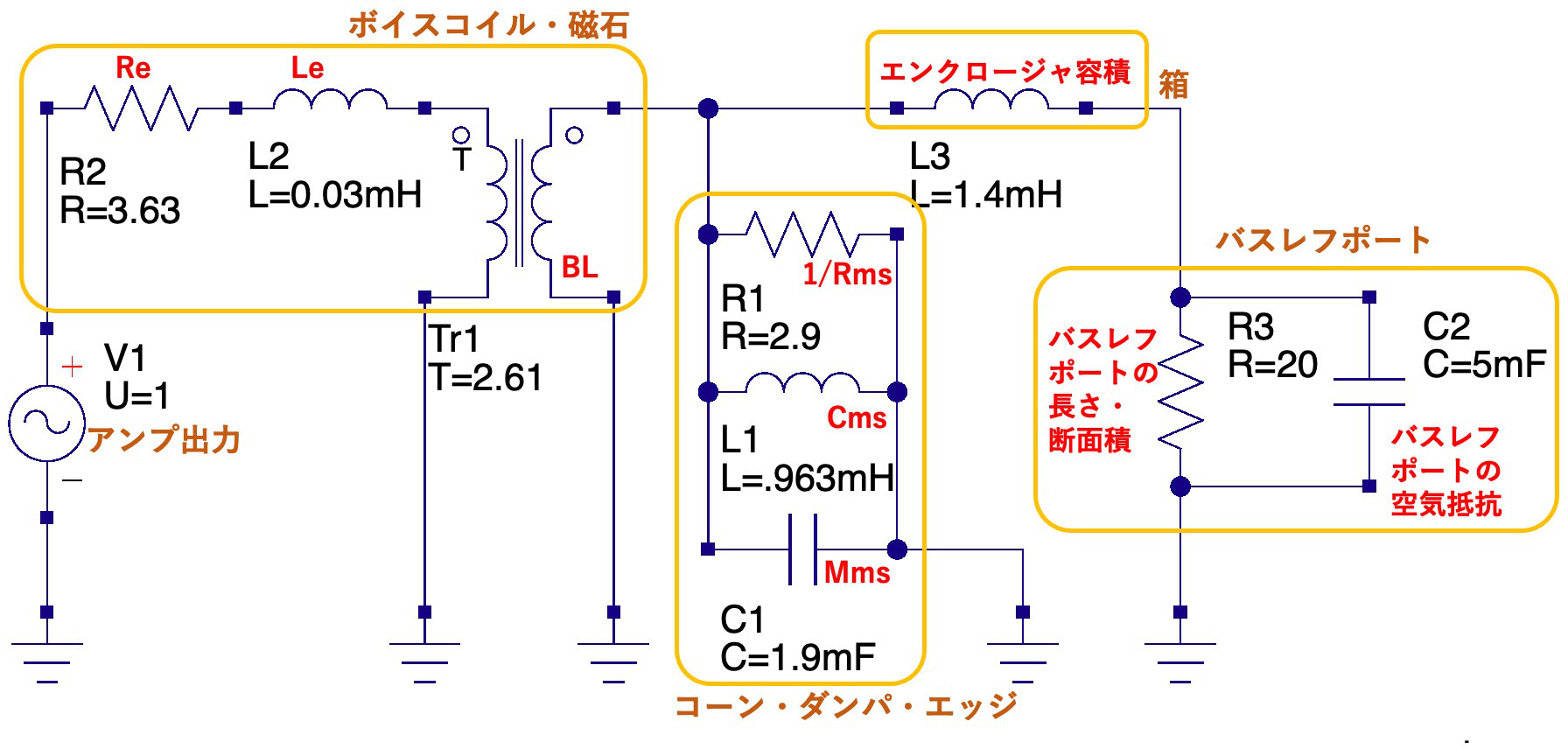
これらのエンクロージャをスピーカユニットの等価回路と組み合わせた回路は上図のようになる.以下では順を追って,エンクロージャ部分の各定数の決定方法を説明する.
密閉型エンクロージャ
密閉型エンクロージャでは背後を密閉するが,コーンが後退するとエンクロージャ内の空気が圧縮されてコーンを押し戻す.これをモデル化する必要がある.今,エンクロージャ内の容積を $V_e [L]$とする.またコーン部分の有効面積は $Sd$ で与えられているため,コーンが 1mm 後退したときの体積変化率は $Sd / V_e \cdot 10^{-4}$となる.また大気圧は $1.03 [kgf/cm^2]$ であるので,これとピストン面積の積を体積変化率と掛け合わせることで,コーンが 1mm 後退したときの力が $ 1.03 \frac{Sd^2}{V_e} 10^{-4} $となる.ただしこれは等温圧縮を仮定している.圧力変化は瞬時に発生するので実際には断熱圧縮となり,比熱比 1.4 がかかる.また $1 [kgf] = 9.8 [N]$ であることと,コイルのインダクタンス $L$ はばね定数 $k$ の逆数であることから,$L = \frac{0.7 V_e}{Sd^2} [H]$と計算できる.

このスピーカに,上のようにガラス瓶を利用した密閉型エンクロージャを取り付けた場合をシミュレーションする.この瓶の容積は 0.9L なので, L = 1.4mH と計算できる.これを組み込んだ等価回路は以下のようになる.
これはバスレフ型・密閉型で共通に利用できる等価回路であり(Qucs のファイルはこちら),エンクロージャ内の空気ばねは L3 で表現されている.C2 と R3 はそれぞれバスレフポート内の空気の質量と抵抗を表しているが,密閉型には穴がないので R3 = 0 としておく.L3 はスピーカ自身のコンプライアンス L1 と並列になっており,あたかもスピーカのばね定数が上がったかのような動作となる(抵抗器と同様に,コイルを並列接続したときの合成インダクタンス $L$ は小さくなる).これにより共振周波数が上がることが知られているが,シミュレーション結果でもインピーダンスのピークが右にずれていることが分かる.また,弾みやすさを表す Q 値も,先に述べた式 $Q = R \sqrt{\frac{C}{L}}$ に従い 0.82 まで上昇し,スピーカ全体としては共振周波数付近が強調され,残響感が安っぽい印象を与えてしまう.
バスレフ型エンクロージャ
次にバスレフ型のスピーカについてシミュレーションする.バスレフポート内の空気は一体となって動き,重りの役割を持つ(ここで問題となる低音は波長が数mと長く,小さなエンクロージャ内では進行波や定在波としては振る舞わない).バスレフポート内の空気は僅かな量であるが,質量としては意外に大きな働きを持つ.というのは,バスレフポートの断面積がコーンの面積よりも小さいためである.つまり,上の図中の「バスレフ型の物理モデル」の右図のように,ちょうど,バスレフポート内の空気はてこの長い方に取り付けられているような状態になっている.バスレフポートの断面積に対するコーンの有効面積の比率を $\alpha$ とすると,コーンの動きに対してバスレフポート内の空気の動きは$\alpha$倍される.これにより,慣性の法則 $F=ma$における加速度 $a$ も $\alpha$ 倍となり,結果的に力 $F$ も $\alpha$ 倍になる.さらにこの圧力がコーン側に戻ったときに力が $\alpha$ 倍される.なぜなら,パスカルの法則により容器内の圧力は一定なので,バスレフポート内の空気が容器内の空気を圧縮する力に対し,それより面積が大きなコーンを押す力は $\alpha$ 倍となるのである.結果的に,バスレフポート内の空気の質量は $\alpha^2$ 倍の効果を持つことになる.空気の質量は 1L あたり 1.2g 程度であるので,バスレフポート長 $L_p [cm]$ (開口補正が必要だがここでは省略する)と断面積 $S_p [cm^2]$ から,空気の質量は $1.2 L_p S_p \cdot 10^{-3}$となる,これに前述の面積比 $\alpha^2 = (\frac{S_d}{S_p})^2$ を掛け,有効質量は $1.2 \cdot 10^{-3} S_d^2 \frac{L_p}{S_p} $となる.つまりバスレフポートは細いほど有効質量が増加し,共振周波数が低くなるのである.
バスレフポート内の空気質量はエンクロージャ内の空気ばねの先にぶら下がっている形なので,電子回路としては,空気ばねの L3 と直列接続となる.またバスレフポート内の空気抵抗 R3 は空気質量と並列接続になる.これは,バスレフポートの場合は低抵抗=大きな値となるが,前述のように 0 にすることで密閉型エンクロージャも表現できる.さらに,中間的な値とすることで非共振型(aperiodic型)のエンクロージャも表現できる.
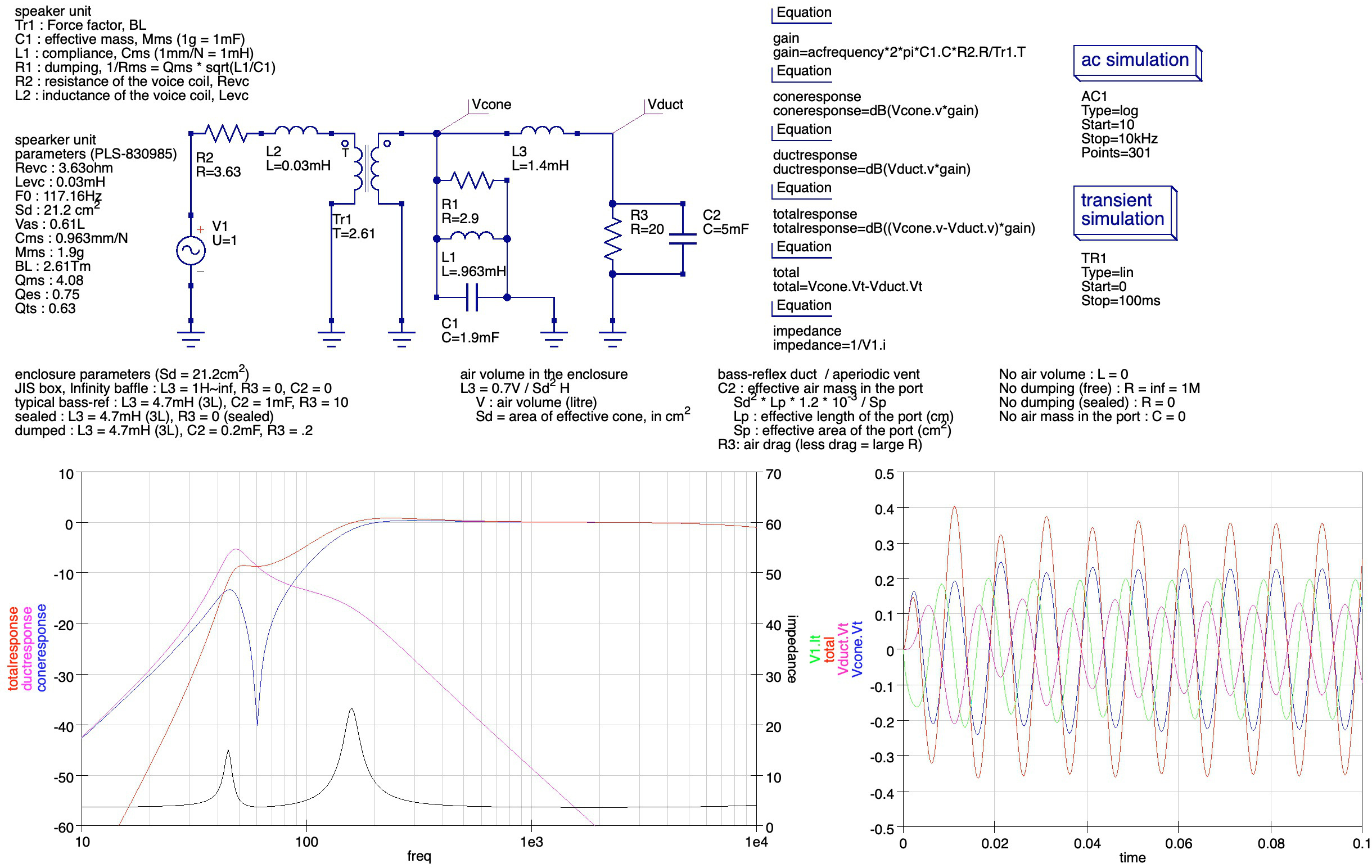
上図は同じエンクロージャにバスレフポートを設けた場合の例である.バスレフポートは,例えば有効長 11cm, 断面積 1cm^2 の場合であるが,実際にはポート壁面の空気は動きにくいことと,開口補正のため,もう少し太く短いポートに相当するだろう.このとき,インピーダンス曲線からも分かるようにスピーカの共振周波数は2つあり,それぞれ異なる動きとなる(共振モードと呼ばれる).下のピーク(43Hzあたり)は,スピーカのコーン紙とバスレフポート内の空気,そしてその間のエンクロージャ内の空気が一斉に,ほぼ同じ方向に動いている場合である.C2 は C1 の約3倍の質量の働きを持ち,これにより共振周波数が小さくなっているが,この場合はバスレフポートからの音圧(紫色で表示:ductResponse)はスピーカ本体からの音圧(青色で表示:coneResponse)と逆相になっているので打ち消し合い,ダクトからの音圧よりも合計の音圧(赤線で表示:totalResponse)が小さくなっている(位相特性を含んだグラフはこちら).ただし,ダクトからの音圧はスピーカ本体からの音圧よりも10dB ほど強くなっている.これは共振の効果である.
もともとあった共振ピークは少し上にずれている(密閉型と合成した画像はこちら).この共振モードでは,コーンとポート内の空気質量が逆の動きをしているためである.このとき,ポートから出力される音圧はスピーカ自身からの音圧に加えられることになり,総合音圧(赤線)はスピーカ単体・ダクト単体それぞれの音圧よりも高くなっている.ただし,単なる密閉型のときに比べてバネ定数が高くなる,つまりエンクロージャが小さくなるのと同じ効果を持ち,共振周波数は密閉型の場合に比べ,さらに少し上に移動する.なぜなら,コーンが下がって背圧が上がったとき,バスレフポート内の空気がエンクロージャ内の空気を同時に押し戻すので,圧力がより高まりやすいいためである.また,Q値もさらに高くなっていることがインピーダンスカーブの比較からも分かる.
バスレフ型では共振現象を積極的に用いており,ダンピングがかかりにくいバスレフポートからの音圧が高くなるため,全体としては低音が増強される.しかしその低音は共振によるものであるため少し遅れること,また,信号が0になってもすぐには止まらないことなどから,締まりのない低音になることがあり嫌われることも多い.よく,アンプの出力インピーダンスを低くして電磁制動により制御する,などと言われるが,図や回路から明らかなように,バスレフポートの共振には電磁制動はほとんど働かない(上のてこの図からも分かるように,コーンを止めても,下の緑色の台車はバネとの間で共振を続けてしまう).ヘルムホルツ共鳴管のQ値は50程度にもなるという(これが低いとバスレフポートによる増強効果が得られない).また,低いほうの共振周波数よりさらに低音側ではバスレフポートとコーンからの音圧がほぼ等しくなり,かつ逆相なので,それらがぴったりと打ち消し合い,急速に減衰してしまう.
密閉型でもバスレフ型でも,エンクロージャ容積が小さすぎるとQ値が上昇し残響感が発生してしまう.さらにバスレフ型では,付け加えられる低域は原音に比べ締まりのないものとなる.
Aperiodic 型エンクロージャ
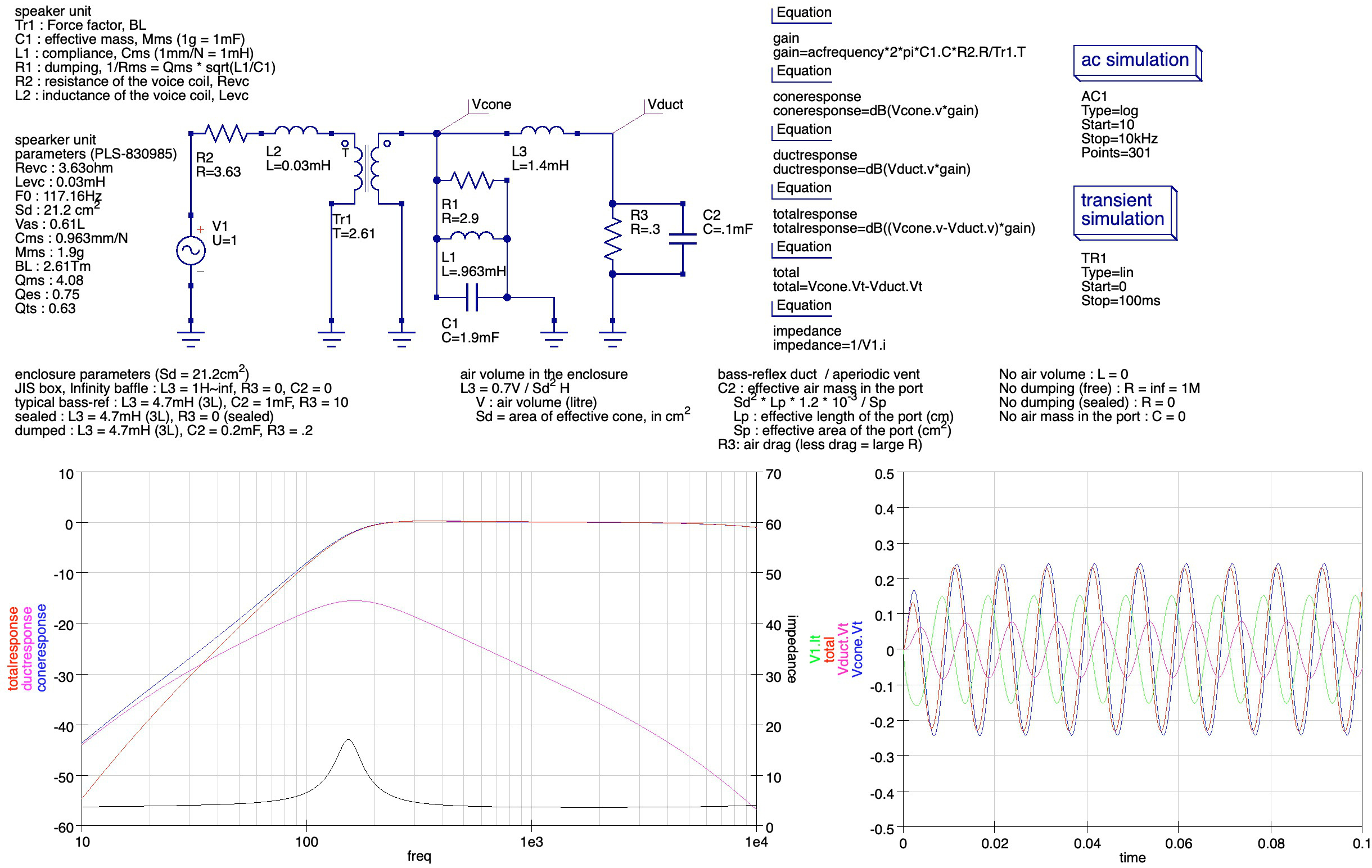
最後に,国内ではほとんど認識されていないが,小型エンクロージャには有効と思われる aperiodic 型エンクロージャについて述べる.このエンクロージャではバスレフ型と同様に空気が抜ける穴があるが,その出口(空気抜きなので,英語では port と呼ばれずに vent と呼ばれることが多いようだ)はできるだけ短く,また直径を大きくすることで共振しづらくする.さらにその出口に綿などの空気抵抗となるものを備えることで,共振を積極的に減衰させる.上の図では R3 がバスレフ型の場合の 1/67 になっているので,抵抗力としては 67 倍となっている.またC2 は 1/50 になっている.これによりコーン紙の共振には制動がかかり,スピーカ単体の場合よりもQ値を低くすることができる,つまり,より共振しづらくなる(それに対し,密閉型,バスレフ型ではどちらも,スピーカ単体よりもQは高くなり,これはエンクロージャが小さいほど顕著である).シミュレーション結果からも,インピーダンスカーブの高さが低くなっていることが分かる(密閉型との比較はこちら).また全体の出力は密閉型に近いが,わずかに低音は弱くなる.周波数が極めて低くなると,空気抵抗の効果が薄れ,ベントからの音圧がコーンからの音圧を打ち消すようになるが,バスレフ型に比べるとその効果は軽微である.それは,ベントからの音圧が小さいことに加え,位相ずれが低域に至るまで残存することによる(位相特性を含んだグラフはこちら).
Q値は0.6 から 0.7 ぐらいが良いとされている.余計な振動が起こらない(行きすぎない)のが Q = 0.5(臨界減衰)であり,これよりもQが大きいと振動がいったりきたりするし,小さいと粘りが強すぎて0に戻るのが遅くなる(粘り気のある油の中に振り子を入れると,振り子が下がりきるまで時間がかかる).振動が最も速く収束するのは Q = 0.707 である.FOSTEX FE103En のような,スピーカユニット単体のQ値(Qts と表記され,機械的Qと電気的Qの合成量である)が小さいユニット(Qts = 0.33)の場合,小さな密閉型スピーカを作っても共振しづらいが(ただし共振周波数は高くなる),今回使用した Pearless PLS-P830985 は単体で Qts = 0.63 と高く,かなり大きなエンクロージャにしなければ共振が耳につく.上のガラス瓶スピーカも計算上は Q = 0.8 前後になるはずだが,実際のユニットはカタログ値よりもQ値が高いらしく共振が耳についたので,中に毛糸(ダンピング効果がある)を詰めて,なんとか聞けるようになったが満足とは言えないものであった.この問題は,aperiodic 型エンクロージャを制作することにより解決することが出来た.