計算尺による単位の変換とカーソルの機能
計算尺では乗除算のほか、三角関数や対数・指数関数などを簡単に計算できるが、ここではその他の典型的な計算や、尺度を組み合わせた計算方法を紹介する。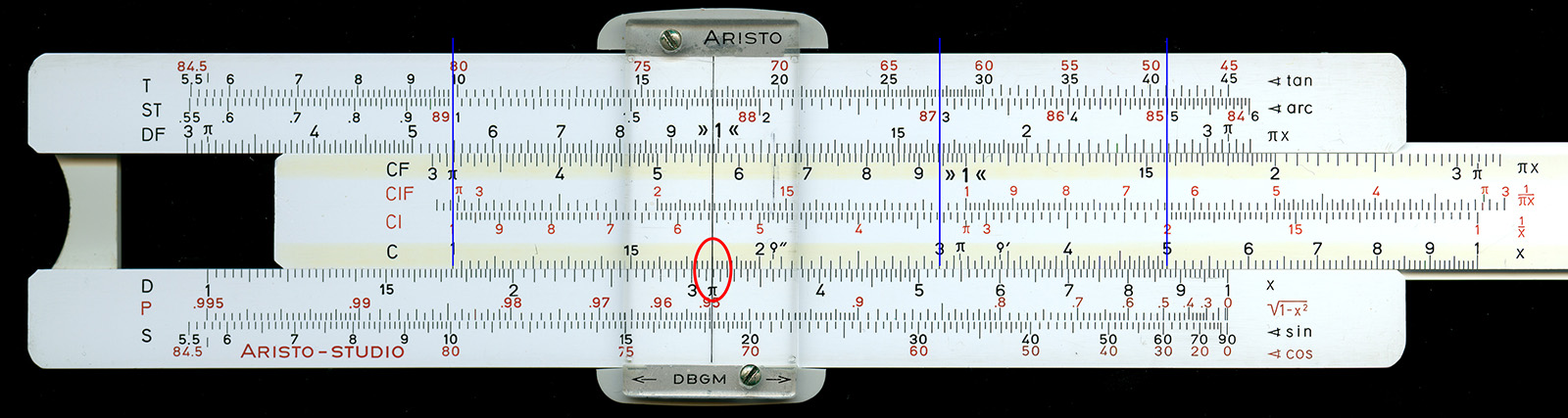
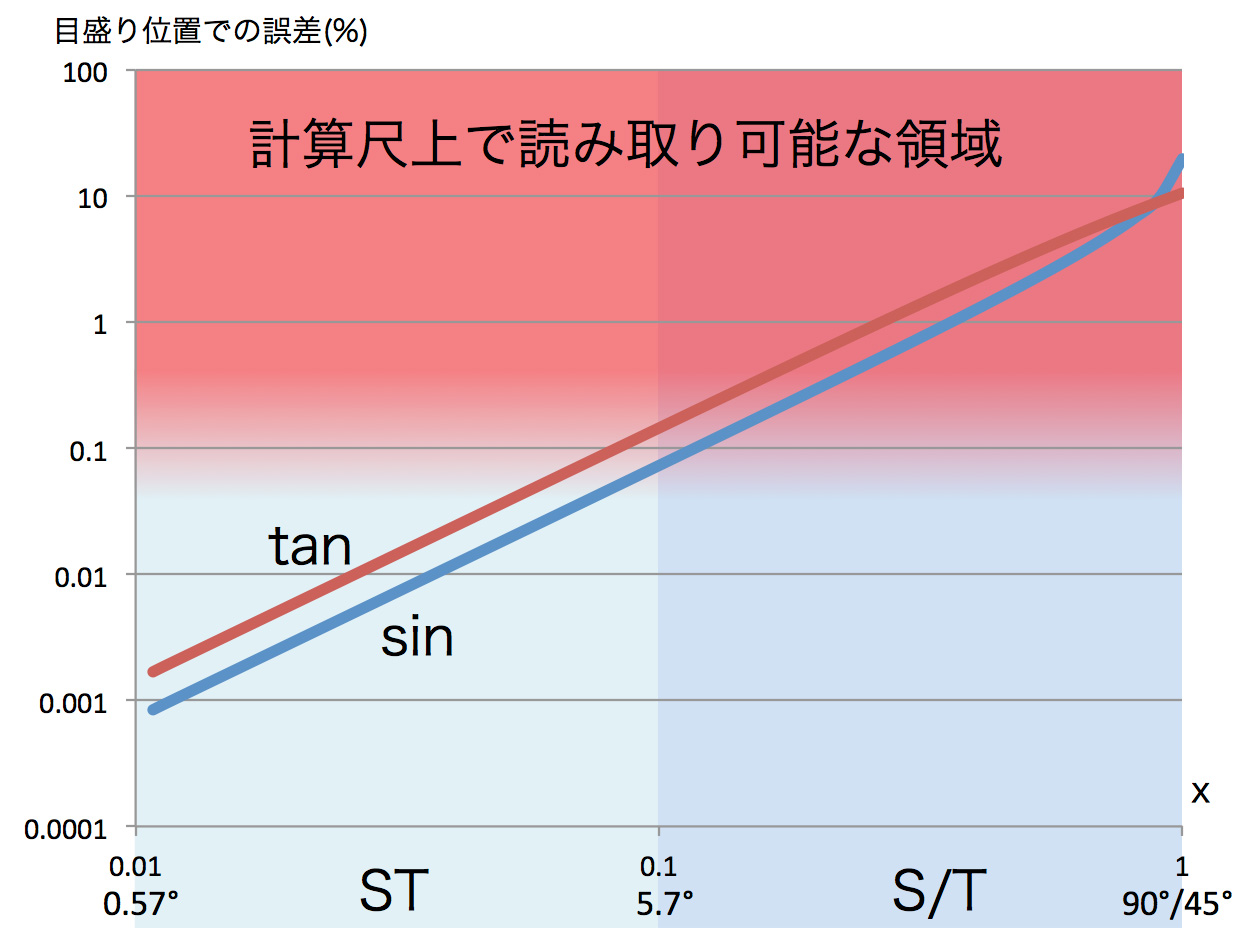
図１ 角度とラジアンの変換
このとき、図１の青線で示すように C 尺と ST 尺の目盛りがほぼ一致する。なぜなら $\theta$[rad] が十分に小さい時、$\sin(\theta) \fallingdotseq \tan(\theta) \fallingdotseq \theta$ という近似が成り立つためである。つまり、例えば ST 尺で $\sin(1^\circ)$ を求めると、その値はD尺上で $0.01745$ であることがわかるが、ST尺を使わなくても図１の方法で $1^\circ$をラジアン単位に変換した値 0.01745 （一番左の青線の D 尺上の値）をそのまま用いれば良いということである。実は ST尺はなくてもほとんど差支えはなく、ST 尺の範囲 $0.57^\circ < \theta < 5.7^\circ$ の範囲で $\sin(\theta)$, $\tan(\theta)$ の値をラジアンへの変換で代用したときの誤差はわずかである（図２）。ましてや、ST 尺より小さな角度 （$0.57^\circ$ 以下）では誤差を気にする必要は全くない。
 図２ $\sin(x)$, $\tan(x)$の計算をラジアン単位への変換で代替したときの誤差。読み取られる数値の誤差ではなく、計算尺の幅全体を100%としたときの目盛りのずれ量を表しており、例えば10インチ（250mm）の計算尺での 0.1% は0.25mm の目盛りのずれに相当する。このようにST尺の範囲では、ラジアン単位への変換でも実用上の誤差は無視できるため $\sin(x)$ と $\tan(x)$ が共用されるが、そもそもこれは角度をラジアン単位へ変換するのと同じである。 |
ちなみに小数点以下７桁までの値を見ると $1^\circ$ は約 $0.0174533$ [rad] で、また $\sin(1^\circ) \fallingdotseq 0.0174524$, $\tan（１^\circ) \fallingdotseq 0.0174551$ である。一方、計算尺ではせいぜい有効数字４桁までしか読めないため、誤差はほぼ無視できることが分かるだろう。また $\sin(\theta) < \theta < \tan(\theta)$ の関係があり、そもそも $\sin(\theta)$ や $\tan(\theta)$ を $\theta$ で近似する誤差よりも、 $\sin(\theta)$ と $\tan(\theta)$ を１つの尺度で兼ねる誤差のほうが大きいのである。そのため実際のところ、ST 尺は $\sin(\theta)$ でも $\tan(\theta)$ でもなく、$\theta$ をラジアンに変換した値（つまり半径１の円弧の長さ arc）そのものが刻まれているのだ。だから、ST尺の備わった計算尺では、角度とラジアンの間の変換はST尺で行えば良い。図１で、D尺の $\pi$ に相当する ST 尺の値（カーソル線上）は $1.8$ になっているのがお分かりだろうか。この関係から、$180^\circ = \pi$ [rad], $18^\circ = 0.1 \pi$ [rad], $1.8^\circ= 0.01 \pi$ [rad] ・・ のように、どの位取りでも正確にラジアンと角度の変換ができる。
長方形の対角線の長さ、複素数の絶対値の計算
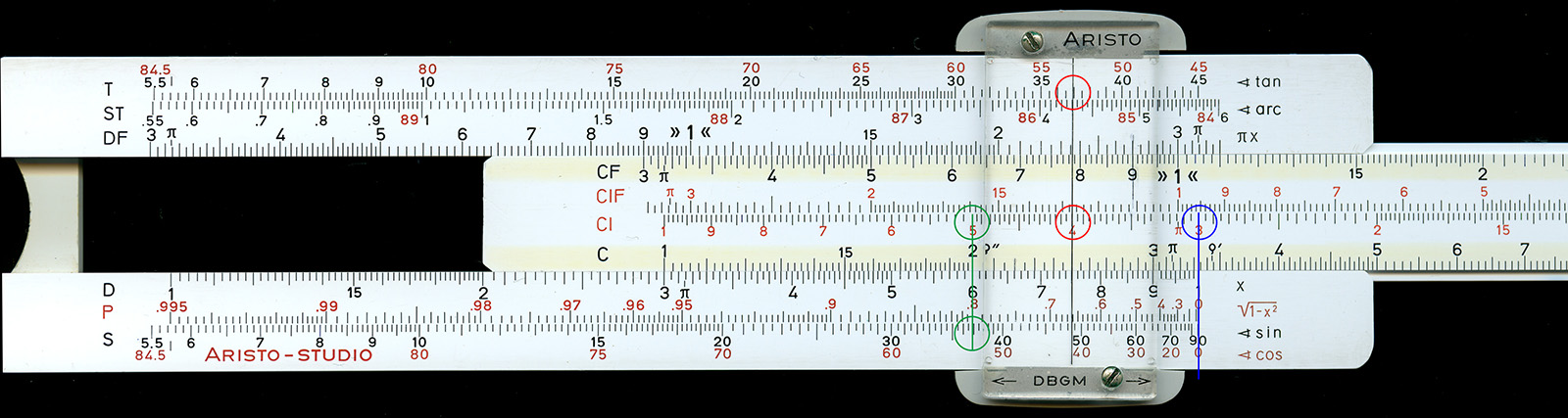
図３ 対角線の長さの計算
まず、２つの辺の長さ $3$ と $4$ のうち、短い方の 3 を CI 尺上で探し、右の基線に合わせる（図３の青丸と青線）。次にもう一方の辺の長さ $4$ を CI 尺上で探し（下の赤丸）、その値に対応する角度 $36.9^\circ$ を T 尺上で求める（カーソル線、上の赤丸）。最後にこの $36.9^\circ$ を S 尺上で探し（下の緑丸）、それに対応する値を CI 尺上で求めると答えの $5$ が得られる（上の緑丸）。
CI 尺を用いなくても、右の基線に C 尺の $4$ をあわせ、$3$ の位置（$0.75$）を読み取ることで $tan^{-1}(3/4)$ を求めることは出来る。しかし最後に $\sin(36.9^\circ)$ から斜辺の長さ $5$ を得るためには、再び滑尺を動かして図２の緑線の位置までC尺の $3$ を持ってくる必要がある（そうすると、右の基線の部分にC尺の $5$ が現れる）。C の逆尺 CI があることで一手間が省けるわけである。
この対角線の長さの計算は、複素数の絶対値を求めたり、ベクトルの長さを求めたりするときにも多用されるので覚えておいて損はない操作法である。なお、辺の長さ 3 : 4 : 5 の直角三角形のうち $3$ と $5$ から $4$ を求めるような操作は逆の手順（ $\sin^{-1}$ を求めてから、その角度の $\tan$ を求める）で可能であるほか、P 尺を用いることで直接的に計算することも出来る。
カーソル線を用いた変換
計算尺のカーソルは、基本的には計算尺上の離れた尺度同士の値を一致させるために用いられる。しかし若干の幅があるため、補助的な線を設けて単位の変換ができるようになっているものが多い。ただしカーソルの幅の制約から、あまり大きな比の変換はできない。
図３ 円の直径からの面積の算出
図４ kW と PS の変換
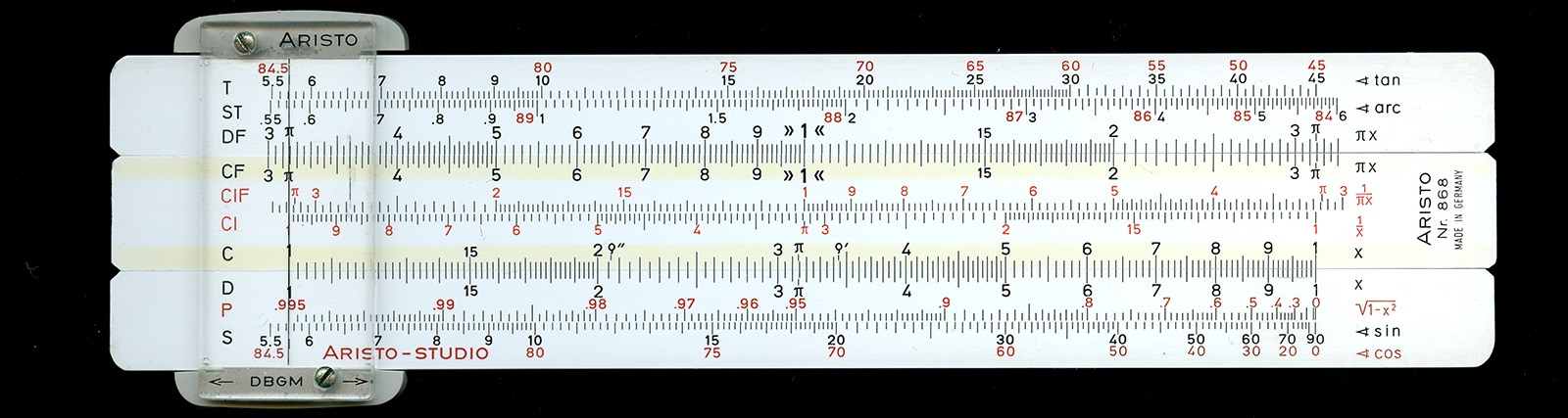
図５ 秒と時間、角度と回転回数、角度と秒などの変換