計算尺の目盛りの種類とその使い方

計算尺の目盛りの種類を尺度と呼ぶ。ここでは別ページで説明した C/D 尺以外の様々な尺度の意味と使い方について解説する。基本となるのは C/D 尺であるので、この上の値を x とし、同じ位置にある他の尺度の値が x に対してどのような値になるのか述べていく。計算尺によっては、それぞれの尺度の左に書かれている計算尺特有の尺度記号の他に、右側に一般的な数式で尺度の意味が書かれているものがあり参考になる。

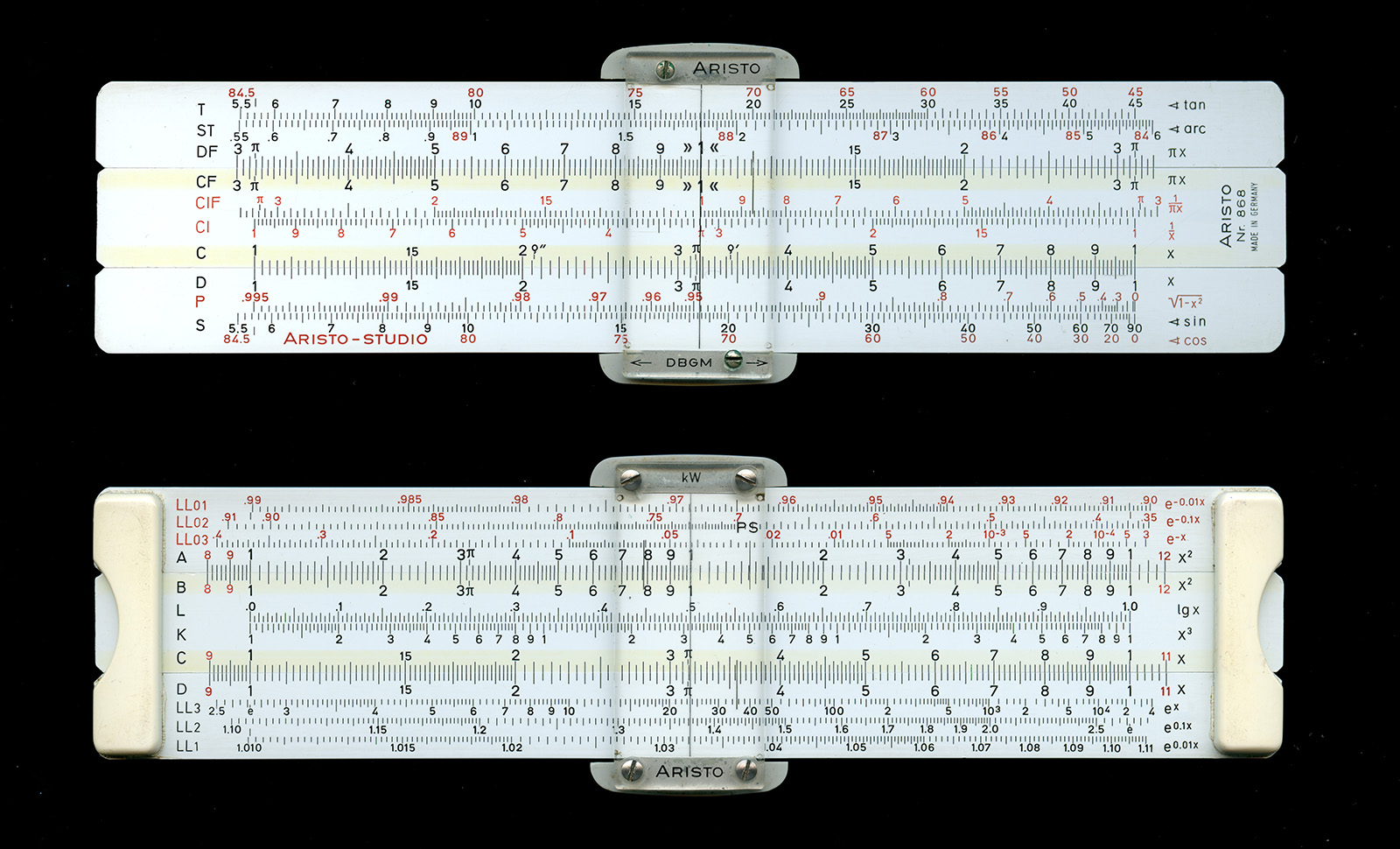
図１　ARISTO-STUDIO Nr. 868

A/B ($x^2$)

$x^2$ の値が刻まれた尺度である。つまり C/D 尺の値と同じところにその値の２乗が現れる。普通A尺はD尺と同じ固定尺上に、またB尺はC尺と同じ滑尺上にある。D尺上の値に対応するA尺の値を読むと２乗ができ、逆にA尺上の値に対応するD尺上の値を読むと平方根が得られる。

A/B 尺は、C/D 尺を半分の長さに縮小して２つ並べたものである。よって A/B 尺でも C/D 尺と同様の乗除算が行える。1～100までの目盛りがあるので、目外れが起こりにくいというメリットがある。

K ($x^3$)

$x^3$ の値が刻まれた尺度である。図１の ARISTO-STUDIO Nr. 868 の場合では C尺の上の値と同じところに、その値の３乗が現れる。C尺の値からK尺を参照すると３乗、逆に参照すると立方根が得られる。目盛りとしては、C/D尺の長さを $1/3$ に縮小して３つ並べたようになっている。

L ($\log_{10}(x)$) / Ln ($\log_e(x)$)

L尺は常用対数 $\log(x)$ の値が刻まれた尺度である。そもそも計算尺とは、$x$ の値の対数 $y = log(x)$ を求め、$0 < y < 1$ の範囲に $x$ の値を刻んでいるため、L尺の値はこの $y$ そのものであり、左端が $0$, 右端が $1$ で、その間が等間隔となっている。C/D尺上の値 $x$ に対し $log(x)$ を求めることができ、逆に L尺上の値 $y$ から $x$ を読むと $x = 10^y$ （例：$10^{0.5} = \sqrt{10} \fallingdotseq 3.16$）が得られる。

L尺を用いて $x^a$ の値を求める事もできる。例えば $x = 2$ のところのL尺の値 $0.3$ を得て、これを $8$ 倍すると $2.4$ になる。この値の小数点以下の値 $0.4$ に対応した $x$ のところの値 $2.51$ を求め、これに整数部 $2$ から求めた $10^2$ をかけて位取りすると $251$ が得られる。$2^8$ の正解は $256$ であり若干の誤差はあるが、概数は求められている。ただしこのような計算は、後で述べる LL 尺を用いたほうが簡単で早い。

数は少ないが、計算尺によっては常用対数（底が $10$。ここでは $\log_{10}(x)$ を $\log(x)$ と書くことにする）の他に、自然対数（底が$e$。ここでは $\log_e(x)$ を $\ln(x)$ と書くことにする）の尺度 Ln を持つもの（例：Pickett N3）もある。

CI/DI (1/x)

C/D尺に対して、左右逆向きに刻んである尺度である。つまりC/D尺上の値 $x$ に対して $1/x$ が得られる。よって C/D 尺上の値 $x_1$ と、その位置にある CI/DI 尺上の値 $x_2$ の積 $x_1 x_2$ が計算尺上でどこでも一定となる。逆数の計算のほか、滑尺やカーソルの移動を最小限にして精度よく、また素早く計算を進める際に便利なことが多い。

CF/DF ($\pi x$ または $x \sqrt{10}$)

C/D尺に対して、半分ずらして置いた尺度である。こちらで述べたように、「目外れ」によって読み取りができなくなることを防ぐために置かれている。ちょうど半分ずらして置く場合、そのずれ量は $\sqrt{10}$ となる（CF/DF尺の右端と左端がともに $\sqrt{10}$ になる。$\sqrt{10}$ 切断という）が、使用上はちょうど半分でなくても良いので、$\pi$ に関する計算が多い工学用の計算尺では $\sqrt{10} \fallingdotseq 3.16$ の代わりに $\pi \fallingdotseq 3.14$ だけずらしてあるものが多い（$\pi$ 切断という）。また計算尺によっては、CF/DF に対応した逆尺である CIF/DIF が刻まれているものもある。

S/T/ST/T₁/T₂ （三角関数）

三角関数に関する尺度である。例えばS尺上の $30^\circ$ の位置に対応する C/D 尺上の値 x を読むと、$x = \sin(30) = 0.5$ が得られる。他の尺度とは逆向きに、S/T/ST/T₁/T₂ 尺から C/D 尺のほうへ読むと三角関数となり、逆に読むと逆三角関数となる。C/D 尺上の値を $0.1 < x < 1$ とすると、S/T/ST/T₁/T₂ 上の値 $\theta$ との関係は以下のようになる（Faber-Castell の計算尺では、C/D 尺上の値を $1 < x < 10$ として数式表記されている）。

S尺 : $x = \sin(\theta)$ ただし $5.7^\circ < \theta < 90^\circ$
ST尺 : $x = 0.1 \sin(\theta)$ または $x = 0.1 \tan(\theta)$ ただし $0.57^\circ < \theta < 5.7^\circ$
T尺/T₁尺 : $x = \tan(\theta)$ ただし $5.7^\circ < \theta < 45^\circ$
T₂尺 : $x = 10 \tan(\theta)$ ただし $45^\circ < \theta < 84.3^\circ$

計算尺によってはオーバーレンジとよび、軽微な目外れを防止したり目盛りを読みやすくするため、右端と左端の1より外側に目盛りが刻んであるものも多い。ST尺が $\sin(\theta)$ と $\tan(\theta) = \sin(\theta)/\cos(\theta)$ で共用なのは、$\theta$ が小さい範囲ではこれらの関数はほぼ同じ値となる（$\cos(\theta) \fallingdotseq 1$である）ためである。また $\theta$ がさらに小さい領域では、$\theta$ をラジアン単位 $r$ に変換すると、$\sin(r) \fallingdotseq \tan(r) \fallingdotseq r = \pi \theta / 180$ と近似できるため、C/D 尺を用いて角度をラジアン単位に変換すればよい。

$0^\circ < \theta < 90^\circ$ の範囲において $\tan(90-\theta) = 1/\tan(\theta)$ が成り立つことから、T₂ 尺は T₁ 尺を左右逆に置いた形となる。そのため多くの計算尺では T₂ がなく、T尺に対し逆向きに $45^\circ < \theta < 84.3^\circ$ の数値を併記し、対応する値は CI 尺で読み取る形式のものも多い。また同様に$0^\circ < \theta < 90^\circ$ の範囲では $\cos(\theta) = \sin(90-\theta)$ であることから、S/ST 尺には $\cos(\theta)$ を求めるための値 $90-\theta$ の数値が併記されているものが多い。

P ($\sqrt{1-x^2}$)

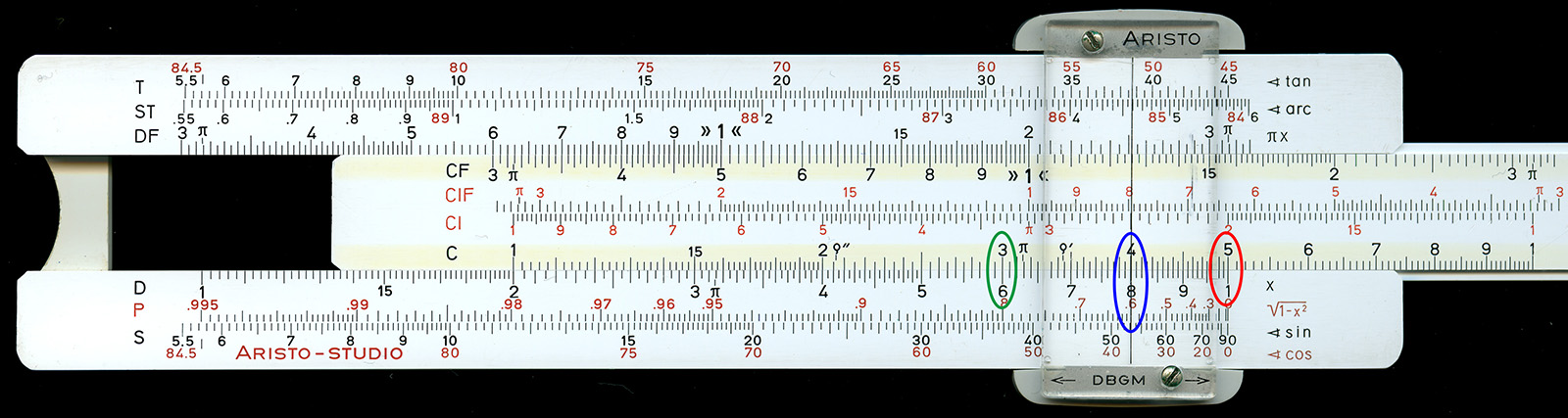
図２　P尺の使い方

ピタゴリアン尺といい、直角三角形に関するピタゴラスの定理 $a^2 + b^2 = c^2$ に関する計算を行う尺度である。計算尺では数値同士の比は C/D 尺を用いて別途計算できるので、 $c = 1$ とすると $a^2 + b^2 = 1$ となり、これを移項して整理した $b = \sqrt{1- a^2}$) を得る。この関数 $\sqrt{1-x^2}$ を求めるのが P 尺であり、$0.1 < x < 1$ の範囲でこの関数の値を求めることが出来る。なお $x < 0.1$ の時は、この関数の値はほぼ $0.995$ 以上となり、$1$ と近似して良い場合が多い。

前述したように P尺はピタゴラスの定理を表したものであるので、直角三角形の辺の長さの関係を求めるのに使用することが出来る。例として、図２は辺の長さが 3 : 4 : 5 の直角三角形について、斜辺の長さ $5$ と１つの辺の長さ $4$ から、残った辺の長さ $3$ を求めるものである。滑尺をずらして右の基線に C 尺の $5$ を合わせる（赤丸）と、$4$ のところ（カーソル上）の D 尺に $0.8 = 4 / 5$ が現れる。この位置の P 尺の値は $0.6$ である（青丸）ため、この値を D 尺上で探し、それに対向した C 尺上の値（緑丸）を読むと $3$ が得られる。

また、斜辺の長さが $1$ の直角三角形は、残り２つの辺の長さがそれぞれ $\sin(\theta)$, $\cos(\theta)$ の関係にあるため、S尺と組み合わせることで $\cos(\theta)$ を求めることが出来る。$\theta$ が $0^\circ$ に近いときの $cos(\theta)$ の値や、$\theta$ が $90^\circ$ に近いときの $\sin(\theta)$ の値は $1.0$ に非常に近く、S 尺単独では精度良く求めることが出来ないが、P尺を用いるとこれを精度良く求めることが出来るというメリットもあり、三角関数と組み合わせて使われることも多い。このため通常、P尺はS尺のそばに置かれる。

P尺には面白い性質として、$\sqrt{1-x^2}$ の逆関数はまた $\sqrt{1-x^2}$ であるため、P尺とC/D尺の上の値はどちらから読んでも同じ値となる点が挙げられる。

LL ($e^x$)

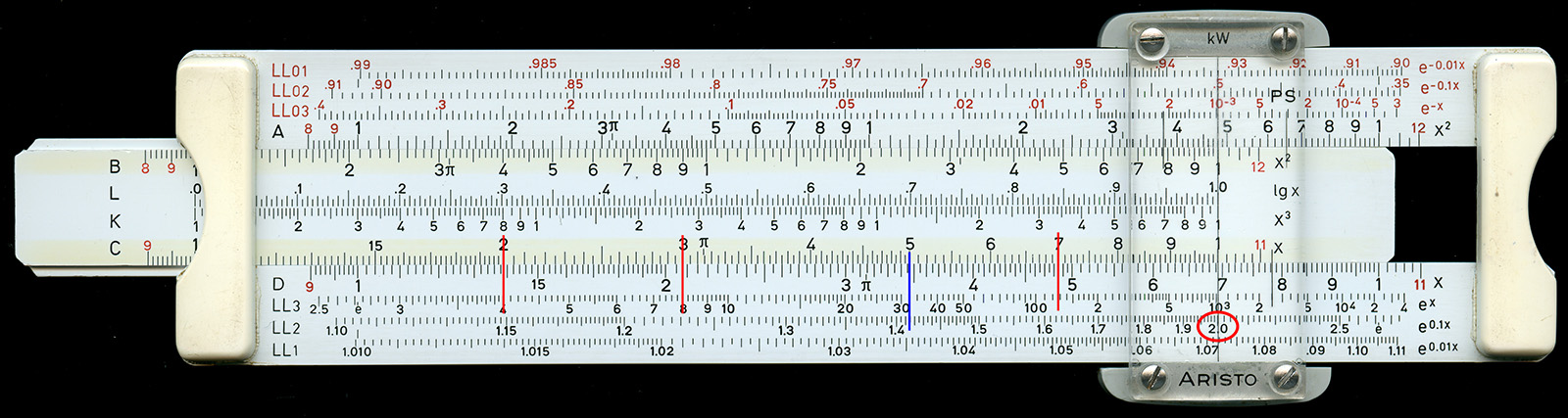
図３　LL尺の使い方

log log 尺と呼ばれ、ある値 $a$ の自然対数の値が C/D 尺で得られるように、つまり $x = \ln(a)$ となるように刻まれた尺度である。この逆関数は $a = e^x$ となるため、例えばLL3 尺に対しての数式表記は $e^x$ となる。log log というが、実際には $y = \log( \ln( a ) )$ のように自然対数と常用対数の合成関数となっている。$1 < x < 10$ の範囲に対する $a$ の範囲は $e < a < 22000$ となるが、より小さい範囲の値も有用であるため、以下のような対応関係で複数の尺度に分けられている場合が多い。

LL3 : $a = e^x$ ただし $1 < x < 10$, $e \fallingdotseq 2.718 < a < 22000$
LL2 : $a = e^x$ ただし $0.1 < x < 1$, $1.1 < a < e$
LL1 : $a = e^x$ ただし $0.01 < x < 0.1$, $1.01 < a < 1.1$
LL0 : $a = e^x$ ただし $0.001 < x < 0.01$, $1.001 < a < 1.01$

また LL03 / LL02 / LL01 / LL00 は、それぞれ LL3 / LL2 / LL1 / LL0 の逆数（$a = e^{-x}$）となっている。

この尺度は、そのまま使うと $a = e^x$ または $x = \ln(a)$ の値が求められるだけであるが、滑尺の移動により任意の値のべき乗、つまり $a^b$ の値を求められるのが特徴である。図３は $2$ のべき乗を求めている様子である。C尺の $1$ をLL2尺の $2.0$ （赤丸）に合わせている。そうすると、C尺上の $2$ の位置に対応する LL3 上に $2^2 = 4$, $3$ の位置に $2^3 = 8$, ・・・, $7$ の位置に $2^7 = 128$, ・・・が現れる（赤線部）。またC尺上の $5$ の位置（青線）に対応する位置には、LL3 上に $2^5 = 32$ が得られており、同時に LL2 上に $2^{0.5} = \sqrt{2} \fallingdotseq 1.414$ が得られる（さらに LL1 上では、$2^{0.05} \fallingdotseq 1.0353$ であることが読み取れる）。このように、LL3 から LL0 までは本来、$0.001 < x < 10$ の範囲について１本に繋がった尺度であると見ることができ、位取りに注意することで容易に大きなべき乗が直読できるようになっている。

理論的には以下のようである。$e^{\alpha b} = (e^{\alpha})^b$ であるため、$a = e^{\alpha}$ となるような $\alpha$ を求めると $a^b$ が得られる。$a = e^{\alpha}$ の逆関数は $\alpha = \ln(a)$ であるため、$\alpha$ はLL尺上の $a$ に対応する値を D 尺上で読み取れば良い。これに $b$ をかけるのに C 尺を用い、再び LL尺に向かって $e^{\alpha b}$ を求めると、この値が求めたい $a^b$ となる。

LL尺は工学用途だけでなく、例えば「年利 2% で 10 年預けると何倍になるか（$1.02^{10} \fallingdotseq 1.219$)」といった複利計算にも便利に使うことが出来る。

計算尺によっては LL0/LL00 がないものがある。しかし $x$ が $0$ に近い時（正でも負でも）、$e^x \fallingdotseq 1 + x$ と良好に近似できるため、実際にはLL0/LL00 尺はなくても差し支えない（図４）。LL 尺で底が $10$ でなく $e$ が用いられているのは、値の範囲の適切さ（Pickett N4 のように底を $10$ にすると、LL3 尺の右端は $10^{10}$ にもなってしまう）のほか、この便利な近似が存在するからである。実際、LL2, LL1, LL0 尺はそれぞれ左端が $1.1$, $1.01$, $1.001$ に近い値となっており、LL1 尺で既に目盛りの配置は D尺に近いものとなっている。LL0 尺になると、その目盛りの配置はほとんど C/D 尺と同じになってしまい、読み取り誤差に埋もれるレベルとなってくる。実際に図５の Faber-Castell 62/83N や 2/83N では LL0 尺と D 尺で目盛りを共用している。

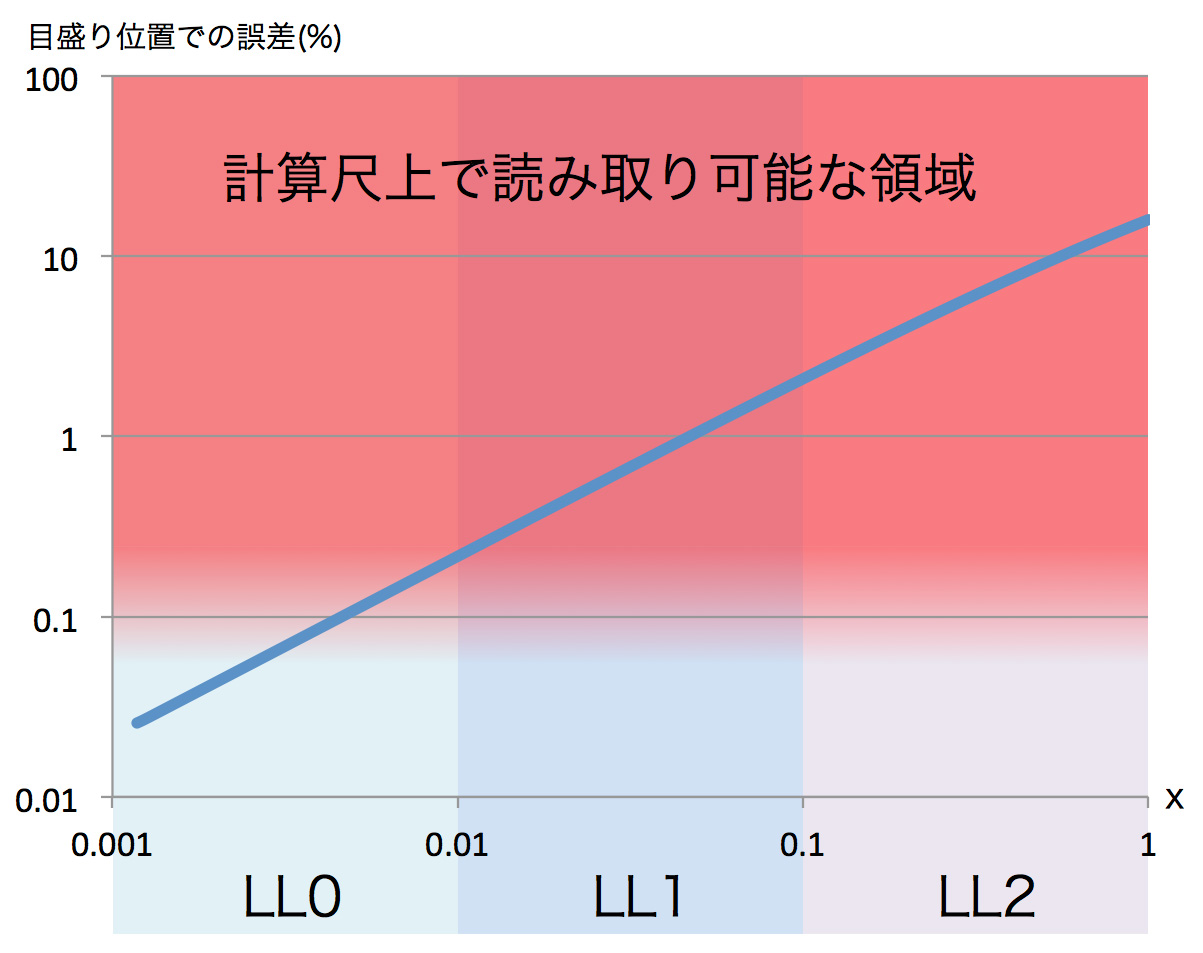図４　LL尺をC/D尺で代替したときの誤差。読み取られる数値の誤差ではなく、計算尺の幅全体を100%としたときの目盛りのずれ量を表しており、例えば10インチ（250mm）の計算尺での 0.1% は0.25mm の目盛りのずれに相当する。読み取られる数値の誤差で言えばもっと小さく、$e^{0.01}$ と $1 + 0.01$ の誤差は 0.005% しかない。

その他

図５　Faber-Castell 62/83N

Faber-Castell の 2/83, 2/83N, 62/83N などでは W₁/W₁', W₂/W₂' が設けられている。これは C/D 尺を倍の長さに伸ばして２つに分割し、滑尺の上下に配置したもので、理論上、倍の精度で計算を行うことが出来るものである。ただし目外れが起こりやすいため、乗除算を行う際に滑尺の基線を置き換える必要が生じることが多い。あわせてL尺も$0$ ～ $1$ でなく $0$ ～ $0.5$, $0.5$ ～ $1$ の範囲が記載されていて倍の精度で読めるようになっている。

Pickett の計算尺では A/B, K 尺とは逆に、x の平方根や三乗根の尺度を持つものがある。A/B, K 尺を用いるよりも高精度であるが、むやみに尺度（目盛り）が増えてしまうという欠点がある。

他にも電子工学や機械工学など分野に特定の尺度を持つ計算尺が多数考案されているが、一般的な計算に用いる尺度は以上のようなものでほぼカバーされる。